题目内容
(本小题满分12分)已知圆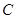 的圆心为原点,且与直线
的圆心为原点,且与直线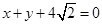 相切。
相切。
(1)求圆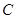 的方程;
的方程;
(2)点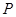 在直线
在直线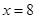 上,过
上,过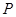 点引圆
点引圆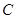 的两条切线
的两条切线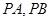 ,切点为
,切点为 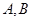 ,求证:直线
,求证:直线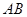 恒过定点。
恒过定点。
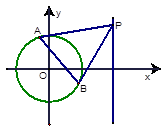
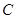 的圆心为原点,且与直线
的圆心为原点,且与直线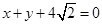 相切。
相切。(1)求圆
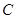 的方程;
的方程;(2)点
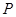 在直线
在直线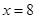 上,过
上,过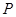 点引圆
点引圆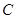 的两条切线
的两条切线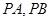 ,切点为
,切点为 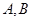 ,求证:直线
,求证:直线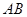 恒过定点。
恒过定点。
解:(1)依题意得:圆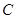 的半径
的半径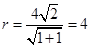 ,所以圆
,所以圆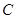 的方程为
的方程为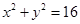 。(4分)
。(4分)
(2)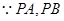 是圆
是圆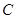 的两条切线,
的两条切线,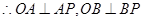 。
。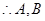 在以
在以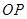 为直径的圆上。
为直径的圆上。
设点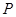 的坐标为
的坐标为 ,则线段
,则线段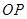 的中点坐标为
的中点坐标为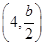 。
。
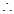 以
以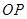 为直径的圆方程为
为直径的圆方程为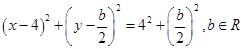 (8分)
(8分)
化简得: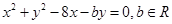
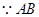 为两圆的公共弦,
为两圆的公共弦,
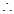 直线
直线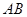 的方程为
的方程为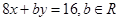
所以直线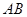 恒过定点
恒过定点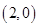 。(12分)
。(12分)
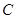 的半径
的半径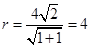 ,所以圆
,所以圆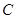 的方程为
的方程为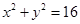 。(4分)
。(4分)(2)
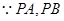 是圆
是圆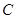 的两条切线,
的两条切线,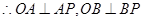 。
。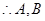 在以
在以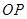 为直径的圆上。
为直径的圆上。设点
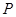 的坐标为
的坐标为 ,则线段
,则线段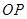 的中点坐标为
的中点坐标为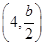 。
。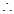 以
以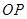 为直径的圆方程为
为直径的圆方程为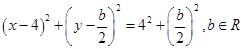 (8分)
(8分)化简得:
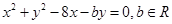
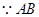 为两圆的公共弦,
为两圆的公共弦, 直线
直线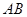 的方程为
的方程为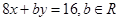
所以直线
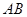 恒过定点
恒过定点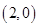 。(12分)
。(12分)略

练习册系列答案
相关题目
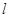 将圆
将圆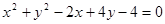 平分,且在两坐标轴上的截距相等,则直线
平分,且在两坐标轴上的截距相等,则直线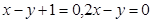
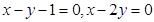
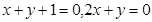
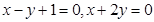
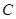 以
以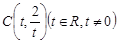 为圆心且经过原点O.
为圆心且经过原点O.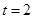 ,写出圆
,写出圆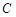 的方程;
的方程;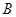 的坐标为
的坐标为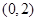 ,设
,设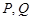 分别是直线
分别是直线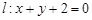 和圆
和圆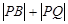 的最小值及此时点
的最小值及此时点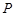 的坐标.
的坐标.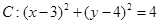 ,直线
,直线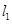 过定点A(1,0).
过定点A(1,0).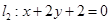 的交点为N,求证:
的交点为N,求证: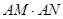 为定值.
为定值.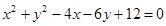 ,
,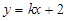 与圆C有两个不同的交点,求
与圆C有两个不同的交点,求 的取值范围.
的取值范围.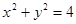
 所围成的较小图形的面积( )
所围成的较小图形的面积( )


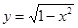 和
和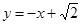 公共点的个数为( )
公共点的个数为( )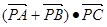 的值是 。
的值是 。 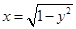 与直线
与直线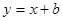 有两个交点,则
有两个交点,则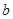 的取值范围是 .
的取值范围是 .