题目内容
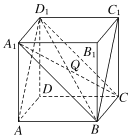
【题目】如图所示,在正方体ABCDA1B1C1D1中,设线段A1C与平面ABC1D1交于点Q,求证:B,Q,D1三点共线.
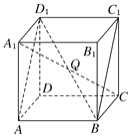
【答案】证明见解析
【解析】
如下图所示,连接A1B,CD1.易证BD1平面A1BCD1. BD1平面ABC1D1.即
平面ABC1D1∩平面A1BCD1=BD1,下证 Q∈平面A1BCD1.Q∈平面A1BCD1.即可.
如下图所示,连接A1B,CD1.显然B∈平面A1BCD1,D1∈平面A1BCD1.
∴BD1平面A1BCD1.
同理BD1平面ABC1D1.
∴平面ABC1D1∩平面A1BCD1=BD1.
∵A1C∩平面ABC1D1=Q,
∴Q∈平面ABC1D1.
又∵A1C平面A1BCD1,
∴Q∈平面A1BCD1.
∴Q∈BD1,即B,Q,D1三点共线.

练习册系列答案
相关题目