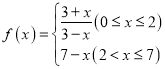题目内容
【题目】设△ABC三个内角A、B、C所对的边分别为![]() 已知
已知![]()
(1)求角B的大小;
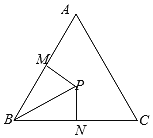
(2)如图,在△ABC内取一点P,使得PB=2,过点P分别作直线BA、BC的垂线PM、PN,垂足分别是M、N,设∠PBA=![]() 求四边形PMBN的面积的最大值及此时
求四边形PMBN的面积的最大值及此时![]() 的值.
的值.
【答案】(1)B![]() (2)α
(2)α![]() 时,四边形PMBN的面积取得最大值
时,四边形PMBN的面积取得最大值![]() .
.
【解析】
(1)由acosA=bcosB及正弦定理可得:sinAcosA=sinBcosB,即sin2A=sin2B,又A∈(0,π),B∈(0,π),可得A=B或A+B![]() . 由于C
. 由于C![]() ,即可得出.
,即可得出.
(2)由题设,在Rt△PMB中,PM=2sinα;PN=2cosα,得其面积;在Rt△PNB中,同理可得PN=2sin(![]() α),PM=2cos(
α),PM=2cos(![]() α),α∈(0,
α),α∈(0,![]() )得其面积,进而得四边形面积,利用恒等变换结合三角函数最值即可得出.
)得其面积,进而得四边形面积,利用恒等变换结合三角函数最值即可得出.
(1)由acosA=bcosB及正弦定理可得:sinAcosA=sinBcosB,
即sin2A=sin2B,又A∈(0,π),B∈(0,π),
∴有A=B或A+B![]() .
.
又∵C![]() ,得A+B
,得A+B![]() ,与A+B
,与A+B![]() 矛盾,
矛盾,
∴A=B,因此B![]() .
.
(2)由题设,得在Rt△PMB中,PM=PBsin∠PBM=2sinα;PN=PBcos∠PBM=2cosα,则![]()
同理,在Rt△PNB中,PN=PBsin∠PBN=PBsin(![]() ∠PBA)=2sin(
∠PBA)=2sin(![]() α),PM=2cos(
α),PM=2cos(![]() α)α∈(0,
α)α∈(0,![]() ),
),![]()
∴四边形PMBN的面积![]()
∵α∈(0,![]() ),∴2α
),∴2α![]() ∈(
∈(![]() ,
,![]() ),
),
于是,当2α![]() ,即α
,即α![]() 时,四边形PMBN的面积取得最大值
时,四边形PMBN的面积取得最大值![]() .
.

【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.