题目内容
6.若存在实数m,n,使得$\left\{\begin{array}{l}{\frac{1}{{e}^{x}}-\frac{a}{x}≥0}\\{x>0}\end{array}\right.$的解集为[m,n],则a的取值范围为( )| A. | ($\frac{1}{{e}^{x}}$,e) | B. | (0,$\frac{1}{{e}^{x}}$) | C. | (0,$\frac{1}{2e}$) | D. | (0,$\frac{1}{e}$) |
分析 由题意得a≤$\frac{x}{{e}^{x}}$,从而令f(x)=$\frac{x}{{e}^{x}}$,f′(x)=$\frac{1-x}{{e}^{x}}$,从而可得0<$\frac{x}{{e}^{x}}$≤$\frac{1}{e}$,从而解得.
解答 解:∵当x>0时,
化简$\frac{1}{{e}^{x}}$-$\frac{a}{x}$≥0得,
$\frac{x-a{e}^{x}}{x•{e}^{x}}$≥0,
即a≤$\frac{x}{{e}^{x}}$,
令f(x)=$\frac{x}{{e}^{x}}$,f′(x)=$\frac{1-x}{{e}^{x}}$,
故f(x)=$\frac{x}{{e}^{x}}$在(0,1]上是增函数,在[1,+∞)上是减函数,
故0<$\frac{x}{{e}^{x}}$≤$\frac{1}{e}$,
结合图象可得,a的取值范围为(0,$\frac{1}{e}$);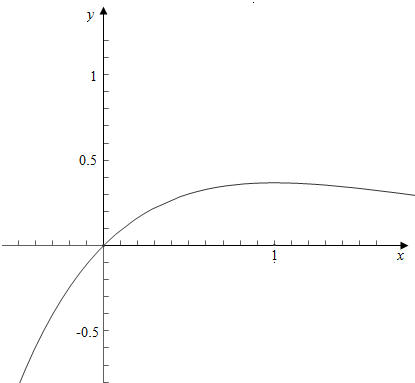
故选D.
点评 本题考查了导数的综合应用及数形结合的思想应用.

练习册系列答案
相关题目
16.平面α⊥平面β的一个充分条件是( )
| A. | 存在一条直线l、l⊥α、l⊥β | B. | 存在一个面r、r∥α、r∥β | ||
| C. | 存在一个平面r、r⊥α、r⊥β | D. | 存在一条直线l、l⊥α、l∥β |
14.三棱锥P-ABC的四个顶点都在球D的表面上,PA⊥平面ABC,AB⊥BC,PA=3,AB=BC=2,则球O的表面积为( )
| A. | 13π | B. | 17π | C. | 52π | D. | 68π |
18.设命题甲:关于x的不等式x2+2ax+4≥0对一切x∈R恒成立,命题乙:设函数f(x)=loga(x-a+2)在区间(1,+∞)上恒为正值,那么甲是乙的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |