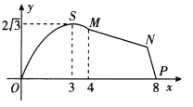
题目内容
【题目】已知![]() ,
,![]() 是函数
是函数![]() (其中常数
(其中常数![]() )图象上的两个动点,点
)图象上的两个动点,点![]() ,若
,若![]() 的最小值为0,则函数
的最小值为0,则函数![]() 的最大值为__________.
的最大值为__________.
【答案】![]()
【解析】
先推出f(x)的图象关于直线x=a对称,然后得出直线PA,PB分别与函数图象相切时,![]()
![]() 的最小值为0,再通过导数的几何意义得切线的斜率,解出a=1,结合图象可得x=1时,f(x)的最大值为
的最小值为0,再通过导数的几何意义得切线的斜率,解出a=1,结合图象可得x=1时,f(x)的最大值为![]() .
.
解:A,B是函数f(x)![]() (其中a>0)图象上的两个动点,
(其中a>0)图象上的两个动点,
当x<a时,f(x)=f(2a﹣x)=﹣e(2a﹣x)﹣2a=﹣e﹣x,
∴函数f(x)的图象关于直线x=a对称.
当点A,B分别位于分段函数的两支上,
且直线PA,PB分别与函数图象相切时,![]()
![]() 的最小值为0,
的最小值为0,
设PA与f(x)=﹣e﹣x相切于点A(x0,y0),
∴f′(x)=e﹣x,∴kAP=f′(x0)=e![]() ,解得x0=a﹣1,
,解得x0=a﹣1,
∵![]()
![]() 的最小值为0,∴
的最小值为0,∴![]() ⊥
⊥![]() ,
,
∴kPA=tan45°=1,∴e![]() 1,∴x0=0,
1,∴x0=0,
∴a=1,∴f(x)max![]() .
.
故答案为:![]()

【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在(195,210]内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图
图1:乙流水线样本频率分布直方图
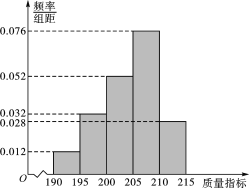
表1:甲流水线样本频数分布表
质量指标值 | 频数 |
(190,195] | 9 |
(195,200] | 10 |
(200,205] | 17 |
(205,210] | 8 |
(210,215] | 6 |
(1)根据图1,估计乙流水线生产产品该质量指标值的中位数和平均数(估算平均数时,同一组中的数据用该组区间的中点值为代表);
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出的不合格品约多少件?