题目内容
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在(195,210]内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图
图1:乙流水线样本频率分布直方图
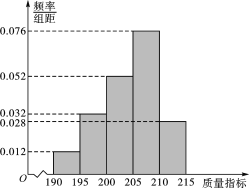
表1:甲流水线样本频数分布表
质量指标值 | 频数 |
(190,195] | 9 |
(195,200] | 10 |
(200,205] | 17 |
(205,210] | 8 |
(210,215] | 6 |
(1)根据图1,估计乙流水线生产产品该质量指标值的中位数和平均数(估算平均数时,同一组中的数据用该组区间的中点值为代表);
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出的不合格品约多少件?
【答案】(1)中位数![]() ,平均数204.5 (2)1500,1000
,平均数204.5 (2)1500,1000
【解析】
(1)根据中位数定义列式求解,再根据组中值求平均数;
(2)先根据古典概型概率分别求甲、乙不合格品概率,再根据概率估计不合格品件数.
解:(1)设乙流水线生产产品的该项质量指标值的中位数为x,
因为0.48=(0.012+0.032+0.052)×5<0.5<(0.012+0.032+0.052+0.076)×5=0.86,
则(0.012+0.032+0.052)×5+0.076×(x-205)=0.5,解得x=![]() .
.
平均数估计为:0.012×5×192.5+0.032×5×197.5+0.052×5×202.5+0.076×5×207.5+0.028×5×212.5=204.5
(2)由甲、乙两条流水线各抽取的50件产品可得,甲流水线生产的不合格品有15件,
则甲流水线生产的产品为不合格品的概率为 P甲=![]() =
=![]() ,
,
乙流水线生产的产品为不合格品的概率为 P乙=(0.012+0.028)×5=![]() ,
,
于是,若某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线生产的不合格品件数分别约为:5000×![]() =1500,5000×
=1500,5000×![]() =1000.
=1000.

【题目】2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有![]() 人,现采用分层抽样的方法,从该单位上述员工中抽取
人,现采用分层抽样的方法,从该单位上述员工中抽取![]() 人调查专项附加扣除的享受情况.
人调查专项附加扣除的享受情况.
(Ⅰ)应从老、中、青员工中分别抽取多少人?
(Ⅱ)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为![]() .享受情况如右表,其中“
.享受情况如右表,其中“![]() ”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
员工 项目 | A | B | C | D | E | F |
子女教育 | ○ | ○ | × | ○ | × | ○ |
继续教育 | × | × | ○ | × | ○ | ○ |
大病医疗 | × | × | × | ○ | × | × |
住房贷款利息 | ○ | ○ | × | × | ○ | ○ |
住房租金 | × | × | ○ | × | × | × |
赡养老人 | ○ | ○ | × | × | × | ○ |
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件
为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件![]() 发生的概率.
发生的概率.