Question

【题目】在直角坐标系中，椭圆关于坐标轴对称，以坐标原点为极点，以轴的正半轴为极轴建立极坐标系， ， 为椭圆上两点.

(1)求直线的直角坐标方程与椭圆的参数方程；

(2)若点在椭圆上，且点在第一象限内，求四边形面积的最大值.

Answer 1

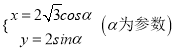【答案】（1）直角方程参数方程为（2）6.

【解析】试题分析：

（1）将点A的坐标化为直角坐标便可得到直线的倾斜角，进而可得直线的方程；然后根据待定系数法可得椭圆的直角坐标方程，再化为参数方程即可．（2）由（1）可得点M(2cosα，2sinα) ，0＜α＜，进而可得点M到直线OA的距离d，所以S＝S△MOA＋S△MOB

＝6sin(α＋)，结合三角知识可得结果．

试题解析：

（1）由A(，)得直线OA的倾斜角为，

所以直线OA斜率为tan＝－1，

故直线OA的方程为，即x＋y＝0．

由x＝ρcosα，y＝ρsinα可得点A的直角坐标为(－， )，

因为椭圆C关于坐标轴对称，且B(2，0)，

所以可设椭圆C：＋＝1，其中t＞0且t≠12，

将(－， )的坐标代入曲线C的方程，可得t＝4，

故椭圆C的方程为，

所以椭圆C的参数方程为．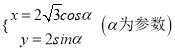

（2）由（1）得M(2cosα，2sinα)，0＜α＜．

点M到直线OA的距离d＝cosα＋sinα．

所以S＝S△MOA＋S△MOB＝(3cosα＋sinα)＋2sinα＝3cosα＋3sinα＝6sin(α＋)，

故当α＝时，四边形OAMB面积S取得最大值6．