题目内容
【题目】知向量![]() ,
,![]() ,函数
,函数![]() ,若
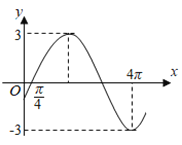
,若![]() 的图象上相邻两条对称轴的距离为
的图象上相邻两条对称轴的距离为![]() ,且图象过点
,且图象过点![]() .
.
(1)求![]() 表达式和
表达式和![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若函数
的图象,若函数![]() 在区间
在区间![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)由题意,求得![]()
![]() ,进而求得
,进而求得![]() ,
,![]() ,即可得到函数的解析式,求得其单调递增区间;
,即可得到函数的解析式,求得其单调递增区间;
(2)根据三角函数的图象变换,得到函数![]() ,进而求得函数
,进而求得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,要使得函数
,要使得函数![]() 在区间
在区间![]() 上有且只有一个零点,只需函数
上有且只有一个零点,只需函数![]() 的图象和直线
的图象和直线![]() 有且只有一个交点,即可求得结论.
有且只有一个交点,即可求得结论.
(1)∵![]()
![]() ,
,
∴![]()
![]() ,
,
∴函数![]() 的最小正周期为
的最小正周期为![]() ,
,
∴![]() ,
,
∵![]() 的图象过点
的图象过点![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
由![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,
∴函数![]() 的单调增区间为
的单调增区间为![]() ,
,![]() .
.
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,可得函数
个单位,可得函数![]()
![]() 的图象;再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
的图象;再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象.
的图象.
∵![]() ,
,
∴![]() ,
,
∴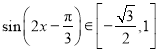 ,
,
∴函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
∵函数![]() 在区间
在区间![]() 上有且只有一个零点,
上有且只有一个零点,
∴函数![]() 的图象和直线
的图象和直线![]() 有且只有一个公共点,
有且只有一个公共点,
根据图象可知,![]() 或
或![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .
.

【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力,某移动支付公司在我市随机抽取了100名移动支付用户进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)在每周使用移动支付超过3次的样本中,按性别用分层抽样的方法随机抽取5名用户.
①求抽取的5名用户中男、女用户各多少人;
②从这5名用户中随机抽取2名用户,求抽取的2名用户中既有男用户又有女用户的概率.
(2)如果认为每周使用移动支付次数超过3次的用户“喜欢使用移动支付”,能否在犯错误概率不超过![]() 的前提下,认为“喜欢使用移动支付”与性别有关?
的前提下,认为“喜欢使用移动支付”与性别有关?
附表及公式:
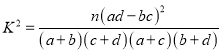
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|