题目内容
【题目】在![]() 中,内角
中,内角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,不等式
,不等式![]() 对一切实数
对一切实数![]() 恒成立.
恒成立.
(1)求![]() 的取值范围;
的取值范围;
(2)当![]() 取最大值,且
取最大值,且![]() 的周长为
的周长为![]() 时,求
时,求![]() 面积的最大值,并指出面积取最大值时
面积的最大值,并指出面积取最大值时![]() 的形状.(参考知识:已知
的形状.(参考知识:已知![]() 、
、![]() ,
,![]() ;
;![]() 、
、![]() ,
,![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() 面积的最大值为
面积的最大值为![]() ,此时
,此时![]() 为等边三角形.
为等边三角形.
【解析】
(1)分![]() 和
和![]() 两种情况讨论,在
两种情况讨论,在![]() 时检验即可,在
时检验即可,在![]() 时,可得出
时,可得出![]() ,由此可求得
,由此可求得![]() 的取值范围;
的取值范围;
(2)由(1)知![]() ,利用余弦定理结合基本不等式可求得
,利用余弦定理结合基本不等式可求得![]() 的最大值,利用等号成立的条件判断
的最大值,利用等号成立的条件判断![]() 的形状,利用三角形的面积公式可求得
的形状,利用三角形的面积公式可求得![]() 面积的最大值.
面积的最大值.
(1)![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,原不等式即为
,原不等式即为![]() 对一切实数
对一切实数![]() 不恒成立;
不恒成立;
当![]() 时,应有
时,应有![]() ,
,![]()
解得![]() 或
或![]() (舍去).
(舍去).
![]() ,则
,则![]() ,所以,
,所以,![]() ,
,
因此,![]() 的取值范围是
的取值范围是![]() ;
;
(2)![]() ,
,![]() ,
,![]() 的最大值为
的最大值为![]() .
.
由余弦定理得![]() ,
,
由基本不等式可得![]() ,
,
![]() (当且仅当
(当且仅当![]() 时,等号成立).
时,等号成立).
![]() 的面积为
的面积为![]() (当且仅当
(当且仅当![]() 时,等号成立).
时,等号成立).
此时,![]() 面积的最大值为
面积的最大值为![]() ,
,![]() 为等边三角形.
为等边三角形.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】某班主任为了对本班学生的月考成绩进行分析,从全班40名同学中随机抽取一个容量为6的样本进行分析.随机抽取6位同学的数学、物理分数对应如表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学分数x | 60 | 70 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 80 | 88 | 90 | 85 | 95 |
(1)根据上表数据用散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?
(2)如果具有线性相关性,求出线性回归方程(系数精确到0.1);如果不具有线性相关性,请说明理由.
(3)如果班里的某位同学数学成绩为50,请预测这位同学的物理成绩。
![]() (附
(附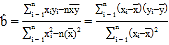 )
)
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() 算得,
算得,![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是 ( )
A. 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别无关”
C. 有99.9%以上的把握认为“爱好该项运动与性别有关”
D. 有99.9%以上的把握认为“爱好该项运动与性别无关”
