Question

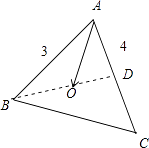
【题目】已知△ABC满足| |=3，| |=4，O是△ABC所在平面内一点，满足| |=| |=| |，且 =λ + （λ∈R），则cos∠BAC= ．

Answer 1

【答案】 或
【解析】解：由| |=| |=| |，可得O是△ABC的外心． ∵ =λ + （λ∈R），∴ ﹣ =（λ﹣1） + ，
即 =（λ﹣1） + =（1﹣λ） + （ ﹣ ）= （ + ）．
设AC的中点为D，则 = 2 =（1﹣λ） ，即B、O、D三点共线．
由于BD⊥AC，∴cos∠BAC= = ．
当λ=0时， = ，此时AB⊥BC，cos∠BAC= = ，
所以答案是： 或 ．

【考点精析】通过灵活运用数量积表示两个向量的夹角，掌握设、都是非零向量，，，是与的夹角，则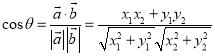即可以解答此题．