题目内容
【题目】(1)在等差数列![]() 中,已知
中,已知![]() ,前
,前![]() 项和为
项和为![]() ,且
,且![]() ,求当
,求当![]() 取何值时,
取何值时, ![]() 取得最大值,并求出它的最大值;
取得最大值,并求出它的最大值;
(2)已知数列![]() 的通项公式是
的通项公式是![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
【答案】(1)当![]() 或
或![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() (2)
(2)![]()
【解析】试题分析:(1)由已知得![]() ,从而
,从而![]() ,进而求出
,进而求出![]() ,根据二次函数的性质可得当
,根据二次函数的性质可得当![]() 或
或![]() 时,
时, ![]() 取得最大值
取得最大值![]() ;(2)由已知得
;(2)由已知得![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,从而数列
的等差数列,从而数列![]() 的前
的前![]() 项和
项和![]() ,由
,由![]() ,得
,得![]() ,从而
,从而![]() 时,
时, ![]() 时,
时, ![]() ,由此能求出数列
,由此能求出数列![]() 的前
的前![]() 项和.
项和.
试题解析: (1)方法一 ∵a1=20,S10=S15,
∴10×20+![]() d=15×20+
d=15×20+![]() d,∴d=-
d,∴d=-![]() .
.
∴an=20+(n-1)×![]() =-
=-![]() n+
n+![]() .
.
∴a13=0,即当n≤12时,an>0,n≥14时,an<0,
∴当n=12或13时,Sn取得最大值,且最大值为S13=S12=12×20+![]() =130.
=130.
(2)∵an=4n-25,an+1=4(n+1)-25,∴an+1-an=4=d,又a1=4×1-25=-21.
所以数列{an}是以-21为首项,以4为公差的递增的等差数列.
令 ,由①得n<6
,由①得n<6![]() ;由②得n≥5
;由②得n≥5![]() ,所以n=6.
,所以n=6.
即数列{|an|}的前6项是以21为首项,公差为-4的等差数列,从第7项起以后各项构成公差为4的等差数列,
而|a7|=a7=4×7-25=3.设{|an|}的前n项和为Tn,则
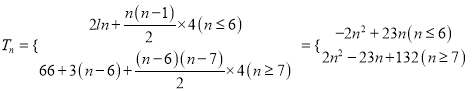

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目