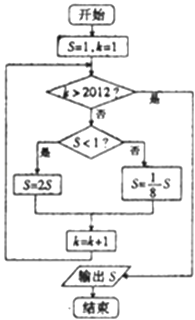
题目内容
【题目】已知动点C到点F(1,0)的距离比到直线x=﹣2的距离小1,动点C的轨迹为E.
(1)求曲线E的方程;
(2)若直线l:y=kx+m(km<0)与曲线E相交于A,B两个不同点,且 ![]() ,证明:直线l经过一个定点.
,证明:直线l经过一个定点.
【答案】
(1)解:由题意可得动点C到点F(1,0)的距离等于到直线x=﹣1的距离,
∴曲线E是以点(1,0)为焦点,直线x=﹣1为准线的抛物线,
设其方程为y2=2px(p>0),∴ ![]() ,∴p=2,
,∴p=2,
∴动点C的轨迹E的方程为y2=4x
(2)证明:设A(x1,y1),B(x2,y2),由 ![]() ,整理得k2x2+(2km﹣4)x+m2=0,
,整理得k2x2+(2km﹣4)x+m2=0,
∴ ![]() ,
, ![]() .
.
∵ ![]() ,
,
∴x1x2+y1y2= ![]() =
= ![]() ,
,
∴m2+4km﹣5k2=0,∴m=k或m=﹣5k,又km<0,m=k舍去,m=﹣5k,满足△=16(1﹣km)>0,
则直线l的方程为y=k(x﹣5),
∴直线l必经过定点(5,0)
【解析】(1)根据抛物线的定义,即可求得曲线E的方程;(2)设直线l的方程,代入抛物线方程,利用韦达定理及向量数量积的坐标运算,求得m=﹣5k,即可求得直线l的方程,则直线l必经过定点(5,0).

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目