题目内容
【题目】已知f(x)=ax2+bx+c(a≠0),满足条件f(x+1)-f(x)=2x(x∈R),且f(0)=1.
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x≥0时,f(x)≥mx-3恒成立,求实数m的取值范围.
【答案】(Ⅰ)f(x)=x2-x+1;(Ⅱ)(-∞,3].
【解析】
(Ⅰ)根据f(0)=1及f(x+1)-f(x)=2x,代入解析式,根据对应位置系数相等,即可求得a、b、c的值,得到f(x)的解析式。
(Ⅱ)将解析式代入不等式,构造函数g(x)=x2-(m+1)x+4,即求当x∈[0,+∞)时g(x) 4≥0恒成立。讨论g(x)的对称轴x=![]() 与0的大小关系,根据对称及单调性即可求得m的取值范围。
与0的大小关系,根据对称及单调性即可求得m的取值范围。
(Ⅰ)由f(0)=1得,c=1,
由f(x+1)-f(x)=2x,得a(x+1)2+b(x+1)+1-(ax2+bx+c)=2x
化简得,2ax+a+b=2x,
所以:2a=2,a+b=1,
可得:a=1,b=-1,c=1,
所以f(x)=x2-x+1;
(Ⅱ)由题意得,x2-x+1≥mx-3,x∈[0,+∞)恒成立.
即:g(x)=x2-(m+1)x+4≥0,x∈[0,+∞)恒成立.
其对称轴x=![]() ,
,
当![]() ≤0,即m≤-1时,g(x)在(0,+∞)上单调递增,
≤0,即m≤-1时,g(x)在(0,+∞)上单调递增,
g(0)=4>0
∴m≤-1成立
②当![]() >0时,
>0时,
满足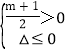
计算得:-1<m≤3
综上所述,实数m的取值范围是(-∞,3].

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”.求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(3)求续保人本年度的平均保费估计值.





