题目内容
14.反比例函数f(x)=$\frac{k}{x}$图象,如图,则( )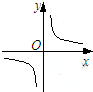
| A. | 常数k<-1 | |
| B. | 函数f(x)在定义域范围内,y随x的增大而减小 | |
| C. | 若点A(-1,m),B(2,n)在f(x)上,则m<n | |
| D. | 函数f(x)图象对称轴的直线方程y=x |
分析 根据反比例函数f(x)的图象与性质,对题目中的选项进行分析判断即可.
解答 解:根据反比例函数f(x)=$\frac{k}{x}$的图象在一、三象限知,k>0,A错误;
又函数f(x)在(-∞,0)和(0,+∞)上是单调减函数,B错误;
当点A(-1,m),B(2,n)在f(x)上时,
m=-k<0,n=$\frac{k}{2}$>0,∴m<n,C正确;
函数f(x)图象对称轴的直线方程为y=±x,∴D错误.
故选:C.
点评 本题考查了函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
7.和圆(x-3)2+(y-1)2=36关于直线x+y=0对称的圆的方程是( )
| A. | (x+1)2+(y+3)2=36 | B. | (x+1)2+(y+3)2=12 | C. | (x-1)2+(y+3)2=36 | D. | (x-1)2+(y-3)2=12 |
19.设全集S={0,2,4,6,8},若A∩B={2},A∩∁SB={0,8},B∩∁SA={4},则下列结论中正确的是( )
| A. | A={0,8} | B. | A∪B={0,2,4,6,8} | C. | ∁SA∩∁SB={6} | D. | ∁SA∪∁SB={6} |
3.过抛物线y2=8x的焦点作圆(x-1)2+y2=4的弦,其中最短的弦长为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
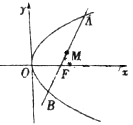 如图,已知抛物线y2=2px(p>0)的焦点为F,过F的直线交抛物线于A、B两点.
如图,已知抛物线y2=2px(p>0)的焦点为F,过F的直线交抛物线于A、B两点.