题目内容
7.和圆(x-3)2+(y-1)2=36关于直线x+y=0对称的圆的方程是( )| A. | (x+1)2+(y+3)2=36 | B. | (x+1)2+(y+3)2=12 | C. | (x-1)2+(y+3)2=36 | D. | (x-1)2+(y-3)2=12 |
分析 先求出圆心和半径,然后根据对称性求出圆心关于直线x+y=0对称的圆的圆心,而圆对称形状不变,从而半径不变,即可求得圆的方程.
解答 解:(x-3)2+(y-1)2=36的圆心为(3,1),半径为6,
点(3,1)关于直线x+y=0对称的点为(-1,-3)
∴圆(x-3)2+(y-1)2=36关于直线x+y=0对称的圆的圆心为(-1,-3),半径为6
即圆的方程为(x+1)2+(y+3)2=36.
故选:A.
点评 本题主要考查了关于直线对称的圆的方程,同时考查了对称点的求解,属于基础题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
14.反比例函数f(x)=$\frac{k}{x}$图象,如图,则( )
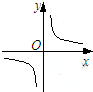

| A. | 常数k<-1 | |
| B. | 函数f(x)在定义域范围内,y随x的增大而减小 | |
| C. | 若点A(-1,m),B(2,n)在f(x)上,则m<n | |
| D. | 函数f(x)图象对称轴的直线方程y=x |