题目内容
对于三次函数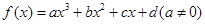 给出定义:
给出定义:
设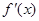 是函数
是函数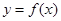 的导数,
的导数,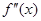 是函数
是函数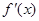 的导数,
的导数,
若方程 有实数解
有实数解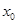 ,则称点
,则称点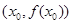 为函数
为函数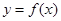 的“拐点”,某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心。给定函数
的“拐点”,某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心。给定函数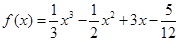 ,请你根据上面探究结果,计算
,请你根据上面探究结果,计算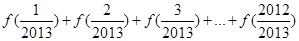 = .
= .
2012
解析试题分析:∵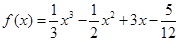 ,
,
∴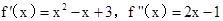 ,
,
令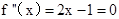 ,得
,得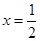 ,
,
∵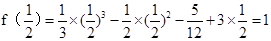 ,
,
∴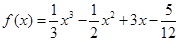 的对称中心为
的对称中心为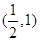 ,
,
∴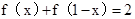 ,
,
∴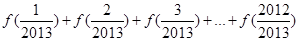 =
=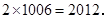
故答案为2012.
考点:导数的计算、函数图象的对称性.

练习册系列答案
相关题目
 为定义在R上的奇函数,当
为定义在R上的奇函数,当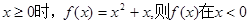 上的解析式为
上的解析式为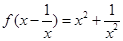 ,则f(3)=___
,则f(3)=___ 是定义在R上的偶函数,当
是定义在R上的偶函数,当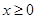 时,
时,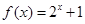 ,若
,若 ,则实数
,则实数 的值为
的值为 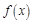 是
是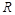 上的单调递增函数,若
上的单调递增函数,若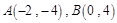 是其图像上的两点,则不等式
是其图像上的两点,则不等式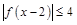 的解集是 .
的解集是 .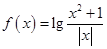
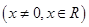 有如下命题:
有如下命题: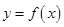 图像关于
图像关于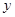 轴对称.
轴对称.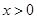 时,
时,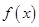 是增函数,
是增函数,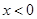 时,
时,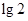 .
. 或
或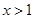 时.
时. 的定义域 .
的定义域 .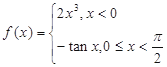 ,则
,则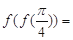 ________.
________.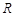 上的函数
上的函数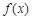 ,对任意
,对任意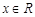 都有
都有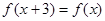 ,当
,当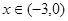 时,
时,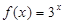 ,则
,则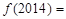 .
.