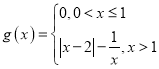题目内容
【题目】已知![]() 为实数,数列
为实数,数列![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)当![]() 和
和![]() 时,分别写出数列
时,分别写出数列![]() 的前5项;
的前5项;
(Ⅱ)证明:当![]() 时,存在正整数
时,存在正整数![]() ,使得
,使得![]() ;
;
(Ⅲ)当![]() 时,是否存在实数
时,是否存在实数![]() 及正整数
及正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ?若存在,求出实数
?若存在,求出实数![]() 及正整数
及正整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)见解析(Ⅱ)见证明;(Ⅲ)见解析
【解析】
(I)利用递推公式,依次计算出![]() 的值.(II)当
的值.(II)当![]() 时,
时,![]() ,此时数列为递减的等差数列,且公差为
,此时数列为递减的等差数列,且公差为![]() ,故总有一项是不大于
,故总有一项是不大于![]() 的.根据这一项在
的.根据这一项在![]() 之间讨论,结合数列的递推公式,判断出正整数
之间讨论,结合数列的递推公式,判断出正整数![]() 存在.(III)将
存在.(III)将![]() 分成
分成![]() 三类,求得
三类,求得![]() 的表达式,由此判断出不存在实数
的表达式,由此判断出不存在实数![]() 正整数
正整数![]() ,使得
,使得![]() .
.
(Ⅰ)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
(Ⅱ)当![]() 时,
时,![]() . 所以,在数列
. 所以,在数列![]() 中直到第一个小于等于
中直到第一个小于等于![]() 的项出现之前,数列
的项出现之前,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的递减的等差数列.
为公差的递减的等差数列.
即![]() .
.
所以,当![]() 足够大时,总可以找到
足够大时,总可以找到![]() ,使
,使![]() .
.
(1)若![]() ,令
,令![]() ,则存在正整数
,则存在正整数![]() ,使得
,使得![]() .
.
(2)若![]() ,因为
,因为![]() ,则
,则![]() ,
,
令![]() ,则存在正整数
,则存在正整数![]() ,使得
,使得![]() .
.
综述所述,则存在正整数![]() ,使得
,使得![]() .
.
(Ⅲ)①当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() (
(![]() ),
),
令![]() ,
,![]() ,而此时
,而此时![]() 为奇数,所以不成立;又
为奇数,所以不成立;又![]() 不成立,所以不存在正整数
不成立,所以不存在正整数![]() ,使得
,使得![]() .
.
②当![]() 时,
时,![]() ……
……
所以数列![]() 的周期是4,
的周期是4,
当![]() ,
,![]() 时,
时,![]() ;
;
当![]() ,
,![]() 时,
时,![]() ;
;
当![]() ,
,![]() 时,
时,![]() ;
;
当![]() ,
,![]() 时,
时,![]() .
.
所以 (
(![]() ).
).
所以![]() 或者是偶数,或者不是整数,即不存在正整数
或者是偶数,或者不是整数,即不存在正整数![]() ,使得
,使得![]() .
.
③当![]() 时,
时,![]()
![]() (
(![]() ),不存在正整数
),不存在正整数![]() ,使得
,使得![]() .
.
综述所述,不存在实数![]() 正整数
正整数![]() ,使得
,使得![]() .
.

练习册系列答案
相关题目