��Ŀ����
����Ŀ��ij��ѧ��ʦ�ڼס�������ƽ�а���á���ͳ��ѧ���͡���Ч���á����ֲ�ͬ�Ľ�ѧģʽ���н�ѧʵ��.Ϊ�˽�̸�ʵЧ�����п��Ժֱ���������и������ȡ![]() ��ѧ������ѧ�ɼ�����ͳ�ƣ��õ����µľ�Ҷͼ��
��ѧ������ѧ�ɼ�����ͳ�ƣ��õ����µľ�Ҷͼ��
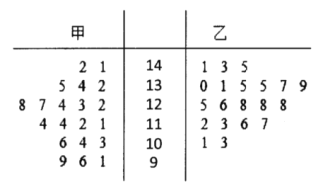
������ס��������ȡ�ķ�������λ���������Ƽס���������ѧ��ƽ��ˮƽ�ͷ�ɢ�̶ȣ���Ҫ����������ֵ���������ۼ��ɣ���
�������涨������![]() ��Ϊ���ã����ѴӼס�������ɼ�Ϊ���õ�ͬѧ�У��÷ֲ���������
��Ϊ���ã����ѴӼס�������ɼ�Ϊ���õ�ͬѧ�У��÷ֲ���������![]() λͬѧ�����ʾ����飬����
λͬѧ�����ʾ����飬����![]() λͬѧ��ǡ���ס�����������
λͬѧ��ǡ���ס�����������![]() �����ϵ�ͬѧ�ĸ���.
�����ϵ�ͬѧ�ĸ���.
���𰸡�����118��128��������������![]() .
.
��������
��������λ���ĸ���ɵó���λ��ֵ���ɾ�Ҷͼ�������ҵ�ƽ��ˮƽ�ͷ�ɢ�̶ȣ����Է������ɣ�
�����ɷֲ�����ĸ���ɵ�Ӧ�Ӽס�����������![]() �ˡ�
�ˡ�![]() �ˣ�����������Ͻ��������¼�ͬʱ�����ĸ��ʹ�ʽȷ�������ʼ���.
�ˣ�����������Ͻ��������¼�ͬʱ�����ĸ��ʹ�ʽȷ�������ʼ���.
�����ݾ�Ҷͼ�ã�
�װ���ͬѧ��������λ����![]() ��
��
�Ұ���ͬѧ��������λ����![]() .
.
�Ұ�ѧ����ѧ���Է�����ƽ��ˮƽ���ڼװ�ѧ����ѧ���Է�����ƽ��ˮƽ��
�װ�ѧ����ѧ���Է����ķ�ɢ�̶ȸ����Ұ�ѧ����ѧ���Է����ķ�ɢ�̶�.
�����ݾ�Ҷͼ��֪��
�ס���������ѧ�ɼ�Ϊ����������ֱ�Ϊ![]() ��
��![]() ������
������![]() �����ϵ���2�ˣ�3�ˣ�
�����ϵ���2�ˣ�3�ˣ�
���÷ֲ���������![]() �ˣ���Ӧ�Ӽס�����������
�ˣ���Ӧ�Ӽס�����������![]() �ˡ�
�ˡ�![]() ��.
��.
�衰�����![]() ����ǡ���мס������������
����ǡ���мס������������![]() �����ϵ�ͬѧ��Ϊ�¼�
�����ϵ�ͬѧ��Ϊ�¼�![]() ��
��
��![]() .
.
�ʣ������![]() ����ǡ���мס������������
����ǡ���мס������������![]() �����ϵ�ͬѧ�ĸ���Ϊ
�����ϵ�ͬѧ�ĸ���Ϊ![]() .
.

 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�