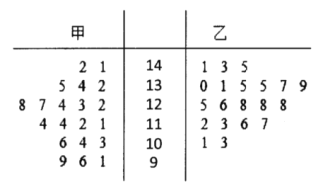
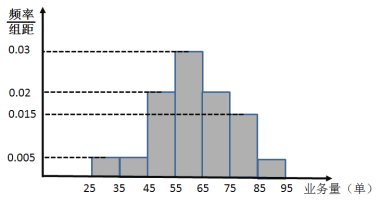
题目内容
【题目】已知抛物线C:y2=2x,过点E(a,0)的直线l与C交于不同的两点P(x1,y1),Q(x2,y2),且满足y1y2=﹣4,以Q为中点的线段的两端点分别为M,N,其中N在x轴上,M在C上,则a=_____.|PM|的最小值为_____.
【答案】2 4![]()
【解析】
过点E(a,0)的直线l的方程设为x=my+a,代入抛物线的方程,运用韦达定理,结合条件,解方程可得a的值;再设直线PM的方程为x=ny+b,联立抛物线方程,设M(x3,y3),运用韦达定理和中点坐标公式,可得b=4,再由弦长公式和二次函数的最值求法,可得所求最小值.
过点E(a,0)的直线l的方程设为x=my+a,代入抛物线方程y2=2x,可得y2﹣2my﹣2a=0,
所以y1+y2=2m,y1y2=﹣2a=﹣4,可得a=2;
设直线PM的方程为x=ny+b,联立抛物线方程y2=2x,
可得y2﹣2ny﹣2b=0,
设M(x3,y3),所以y1+y3=2n,y1y3=﹣2b,
由Q为MN的中点,且N在x轴上,可得y3=2y2,
即有2y1y2=﹣2b=﹣8,可得b=4,
则|PM|![]()
![]()
![]() 2
2![]()
![]() 2
2![]() 4
4![]() ,
,
当n=0即PM⊥x轴时,|PM|取得最小值4![]() .
.
故答案为:2;4![]() .
.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目