题目内容
【题目】武汉出现的新型冠状病毒是一种可以通过飞沫传播的变异病毒,某药物研究所为筛查该新型冠状病毒,需要检验血液是否为阳性,现有![]() 份血液样本,每份样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验n次;②混合检验,将其中
份血液样本,每份样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验n次;②混合检验,将其中![]() 份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份血液全为阴性,因此这k份血液样本检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为
份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份血液全为阴性,因此这k份血液样本检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阴性还是阳性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阴性还是阳性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份为阳性,若采取逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中![]() 份血液样本,记采用逐份检验方式,样本需要检验的次数为
份血液样本,记采用逐份检验方式,样本需要检验的次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(i)试运用概率统计知识,若![]() ,试求P关于k的函数关系式
,试求P关于k的函数关系式![]() ;
;
(ii)若![]() ,采用混合检验方式可以使得这k份血液样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
,采用混合检验方式可以使得这k份血液样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
【答案】(1) ![]() ;(2) (i)
;(2) (i)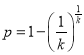 ,
,![]() ;(ii)4
;(ii)4
【解析】
(1)根据排列的方法列式求概率即可.
(2) (i)分别求解![]() ,再化简求
,再化简求![]() 时
时![]() 的解析式即可.
的解析式即可.
(ii)由题![]() ,化简可得
,化简可得![]() ,再构造函数求导分析函数的单调性,再根据零点存在性定理求区间端点的正负判断即可.
,再构造函数求导分析函数的单调性,再根据零点存在性定理求区间端点的正负判断即可.
(1)设恰好经过2次检验能把阳性样本全部检验出来的事件为![]() ,则
,则![]() ,故恰好经过2次检验能把阳性样本全部检验出来的概率为
,故恰好经过2次检验能把阳性样本全部检验出来的概率为![]()
(2) (i)由已知可得![]() ,
,![]() 所有可能的取值为
所有可能的取值为![]() .
.
所以![]() ,
,![]() ,
,
所以![]() .
.
若![]() ,则
,则![]() ,所以
,所以![]() .
.
故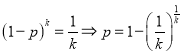 .
.
所以P关于k的函数关系式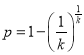 ,
,![]()
(ii)由题意可知![]() ,即
,即![]() ,化简得
,化简得![]() .
.
因为![]() ,所以
,所以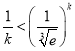 ,即
,即![]() .
.
设函数![]() .
.
又![]() ,故当
,故当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
,![]() .
.
故![]() 的最大值为4.
的最大值为4.


