题目内容
已知函数 ,其中
,其中 为实数,若
为实数,若 对
对 恒成立,且
恒成立,且 ,则
,则 的单调递增区间是
的单调递增区间是
A. | B. |
C. | D. |
C
解析试题分析:因为 对
对 恒成立,即
恒成立,即 ,所以
,所以 ;而
;而 得
得 ,因此得
,因此得 ,所以
,所以 ,根据函数的单调性可求得C为正确答案.
,根据函数的单调性可求得C为正确答案.
考点:三角函数的运算、三角函数的性质.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
函数 的零点个数是( )
的零点个数是( )
| A.0 | B.l | C.2 | D.4 |
已知减函数 是定义在
是定义在 上的奇函数,则不等式
上的奇函数,则不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
若直角坐标平面内 两点满足条件:①点
两点满足条件:①点 都在
都在 的图象上;②点
的图象上;②点 关于原点对称,则对称点对
关于原点对称,则对称点对 是函数的一个“兄弟点对”(点对
是函数的一个“兄弟点对”(点对 与
与 可看作一个“兄弟点对”).已知函数
可看作一个“兄弟点对”).已知函数 , 则
, 则 的“兄弟点对”的个数为( )
的“兄弟点对”的个数为( )
| A.2 | B.3 | C.4 | D.5 |
方程 的解所在的区间是( )
的解所在的区间是( )
A. | B. | C. | D. |
已知函数 为奇函数,且当
为奇函数,且当 时,
时, ,则
,则 =( )
=( )
| A.2 | B.1 | C.0 | D.-2 |
函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)= ( ).
| A.ex+1 | B.ex-1 | C.e-x+1 | D.e-x-1 |
 和
和 是同一函数;②函数
是同一函数;②函数 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为 ;③函数
;③函数 的递增区间为
的递增区间为 ;④若函数
;④若函数 的最大值为3,那么
的最大值为3,那么 的最小值就是
的最小值就是 .
. 切直线
切直线 于
于 点,射线
点,射线 从
从 出发绕着
出发绕着 ,旋转过程中
,旋转过程中 ,记
,记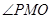 为
为 ,弓形
,弓形 的面积
的面积 ,那么
,那么 的大致图象是 ( )
的大致图象是 ( )
