题目内容
已知减函数 是定义在
是定义在 上的奇函数,则不等式
上的奇函数,则不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
B
解析试题分析:因为函数 是定义在
是定义在 上的奇函数,所以有函数
上的奇函数,所以有函数 过点
过点 ,所以
,所以 ,又因为
,又因为 在
在 上为减函数,不等式
上为减函数,不等式 ,故选B.
,故选B.
考点:本题考查利用抽象函数的性质解不等式.

练习册系列答案
相关题目
定义: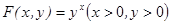 ,已知数列
,已知数列 满足:
满足:
 ,若对任意正整数
,若对任意正整数 ,都有
,都有
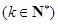 成立,则
成立,则 的值为( )
的值为( )
A. | B. | C.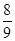 | D. |
函数 是( )
是( )
A.最小正周期为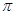 的偶函数 的偶函数 |
B.最小正周期为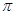 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的奇函数 的奇函数 |
已知函数 ,其中
,其中 为实数,若
为实数,若 对
对 恒成立,且
恒成立,且 ,则
,则 的单调递增区间是
的单调递增区间是
A. | B. |
C. | D. |
已知定义域为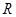 的奇函数
的奇函数 .当
.当 时,
时,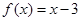 ,则不等式
,则不等式 的解集为( )
的解集为( )
A. | B. |
C. | D. |
已知定义在R上的函数y=f(x)满足以下三个条件:①对于任意的x∈R,都有f(x+4)=f(x);②对于任意的x1,x2∈R,且0≤x1<x2≤2,都有f(x1)<f(x2);③函数y=f(x+2)的图象关于y轴对称.则下列结论中正确的是( ).
| A.f(4.5)<f(7)<f(6.5) | B.f(7)<f(4.5)<f(6.5) |
| C.f(7)<f(6.5)<f(4.5) | D.f(4.5)<f(6.5)<f(7) |
已知f(x)是定义在R上的奇函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2]时,f(x)=ex-1,则f(2 013)+f(-2 014)=( ).
| A.1-e | B.e-1 |
| C.-1-e | D.e+1 |
已知 ,
, ,则函数
,则函数 的图象必定不经过( )
的图象必定不经过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
 的图象大致是( )
的图象大致是( )