题目内容
(本小题12分)某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件。由于市场饱和顾客要求提高,公司计划投入资金进行产品升级。据市场调查,若投入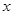 万元,每件产品的成本将降低
万元,每件产品的成本将降低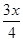 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(Ⅰ)求 的函数解析式;
的函数解析式;
(Ⅱ)求 的最大值,以及
的最大值,以及 取得最大值时
取得最大值时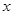 的值.
的值.
(1)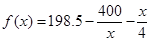 (2)
(2) 的最大值为万元
的最大值为万元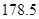 ,
,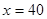 万元
万元
解析试题分析:⑴依题意,产品升级后,每件的成本为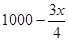 元,利润为
元,利润为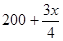 元
元
年销售量为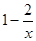 万件 ……3分,
万件 ……3分,
纯利润为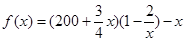 ……5分,
……5分, ……7分
……7分
⑵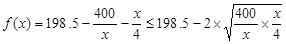 ……9分,
……9分,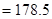 ……10分,
……10分,
等号当且仅当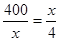 ……11分,
……11分,
即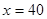 (万元) ……12分
(万元) ……12分
考点:本小题主要考查以基本不等式为工具求函数的最值.
点评:求解这种实际问题时,首先要耐心读懂题目,根据题目写出函数解析式,并且注意实际问题的定义域;利用基本不等式求最值时,要注意基本不等式成立的条件:一正二定三相等.

 名校课堂系列答案
名校课堂系列答案(本小题满分14分)某公司生产的新产品的成本是2元/件,售价是3元/件,
年销售量为10万件,为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是 (万元)时,产品的销售量将是原销售量的
(万元)时,产品的销售量将是原销售量的 倍,且
倍,且 是
是 的二次函数,它们的关系如下表:
的二次函数,它们的关系如下表:
 | ··· | 1 | 2 | ··· | 5 | ··· |
 | ··· | 1.5 | 1.8 | ··· | 1.5 | ··· |
(2)求
 与
与 的函数关系式;
的函数关系式;(3)如果利润=销售总额
 成本费
成本费 广告费,试写出年利润S(万元)与广告费
广告费,试写出年利润S(万元)与广告费 (万元)的函数关系式;并求出当广告费
(万元)的函数关系式;并求出当广告费 为多少万元时,年利润S最大.
为多少万元时,年利润S最大. 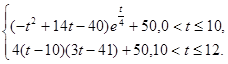
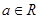 且
且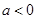 ,设函数
,设函数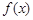 = ax2 +x-3alnx.
= ax2 +x-3alnx. 的单调区间;
的单调区间;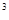 ,池底和池壁的造价分别为2
,池底和池壁的造价分别为2 元/
元/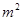 、
、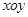 中,设二次函数
中,设二次函数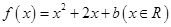 的图象与两坐标轴有三个交点,经过这三个交点的圆记为
的图象与两坐标轴有三个交点,经过这三个交点的圆记为 .求:
.求: 的取值范围;
的取值范围;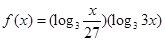
 ,求函数
,求函数 最大值和最小值;
最大值和最小值;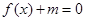 有两根
有两根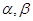 ,试求
,试求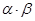 的值.
的值.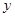 (毫克)与时间
(毫克)与时间 (小时)满足:前1小时内成正比例递增,1小时后按指数型函数
(小时)满足:前1小时内成正比例递增,1小时后按指数型函数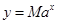 (
(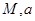 为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.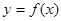 的解析式;
的解析式;