题目内容
(文科题)(本小题12分)
要建造一个无盖长方体水池,底面一边长固定为8m,最大装水量为72m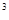 ,池底和池壁的造价分别为2
,池底和池壁的造价分别为2 元/
元/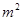 、
、 元/
元/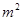 ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
水池底的另一边长为3m,水池的高为3m时,水池的总造价最低,最低造价是114a元。
解析试题分析:设水池底另一边长b,高h,则8bh=72,即bh=9.总造价S=2a•8b+a•2•(bh+8h)=(b+h)•16a+18a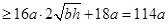 。由此能求出水池底边和高均为3米时,水池造价最低,最低造价是114a.
。由此能求出水池底边和高均为3米时,水池造价最低,最低造价是114a.
设池底另一边长为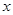 m,水池高为
m,水池高为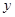 m,总造价为
m,总造价为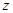 元………………1分
元………………1分
依题意,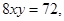
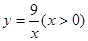 …………………3分
…………………3分
当且仅当 时,…………………10分
时,…………………10分
总造价最低,最低 ………………………11分
………………………11分
答;水池底的另一边长为3m,水池的高为3m时,水池的总造价最低,最低造价是114a元。……12分
考点:函数的模型的选择与应用.函数在生产实际中的应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想
点评:.本题综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意均值定理的灵活运用.

练习册系列答案
相关题目
 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为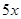 吨和
吨和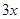 吨。
吨。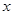 的函数;
的函数;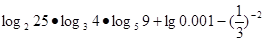
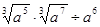
 ,
, ,
,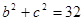 ,
, 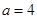 .
.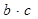 的最大值及
的最大值及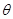 的取值范围;
的取值范围;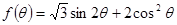 的最值. (本题满分12分)
的最值. (本题满分12分)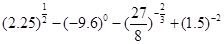 ;
;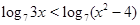 .
.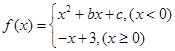 ,若
,若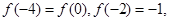
 的解析式;
的解析式; 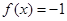 ,求相应
,求相应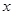 的值.
的值.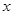 万元,每件产品的成本将降低
万元,每件产品的成本将降低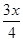 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本) 满足
满足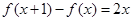 ,且
,且 .(1)求
.(1)求 的解析式;(2)若在区间
的解析式;(2)若在区间 上,不等式
上,不等式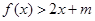 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.