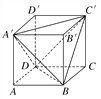
题目内容
【题目】如图所示的几何体中,ABC﹣A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°. 
(1)若AA1=AC,求证:AC1⊥平面A1B1CD;
(2)若CD=2,AA1=λAC,二面角A﹣C1D﹣C的余弦值为 ![]() ,求三棱锥C1﹣A1CD的体积.
,求三棱锥C1﹣A1CD的体积.
【答案】
(1)证明:连接A1C交AC1于E,因为AA1=AC,又A A1⊥平面ABCD,所以AA1⊥AC,
所以A1ACC1为正方形,所以A1C⊥AC1,
在△ACD中,AD=2CD,∠ADC=60°,由余弦定理得 AC2=AD2+CD2﹣2 ACDCcos60°,
所以 ![]() ,所以AD2=AC2+CD2,
,所以AD2=AC2+CD2,
所以CD⊥AC,又AA1⊥CD.所以CD⊥平面A1ACC1,
所以CD⊥AC1,所以AC1⊥平面A1 B1CD.
(2)如图建立直角坐标系,则D(2,0,0), ![]() ,
, ![]() ,
, ![]() ∴
∴ ![]() ,
, ![]()
对平面 AC1D,因为 ![]() ,
, ![]()
所以法向量 ![]() ,
,
平面C1CD的法向量为 ![]() ,
,
由 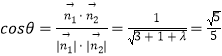 ,得λ=1,
,得λ=1,
所以 A A1=AC,此时,CD=2, ![]() ,
,
所以 ![]()
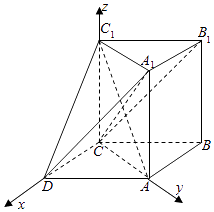
【解析】(1)连接A1C交AC1于E,证明AA1⊥AC,CD⊥AC,推出CD⊥平面A1ACC1 , 然后证明AC1⊥平面A1 B1CD.(2)如图建立直角坐标系,求出相关点的坐标,求出平面 AC1D的法向量 ![]() ,平面C1CD的法向量为
,平面C1CD的法向量为 ![]() ,通过向量的数量积求出λ=1,然后利用等体积法求解体积即可.
,通过向量的数量积求出λ=1,然后利用等体积法求解体积即可.
【考点精析】关于本题考查的直线与平面垂直的判定,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.

【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.