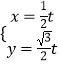题目内容
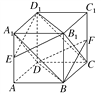
【题目】如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
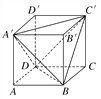
(1)三棱锥A′-BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′-BC′D的体积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)三棱锥A′BC′D为正四面体,表面积为四个正三角形面积,边长为正方体棱长![]() 倍,根据三角形面积公式以及正方形面积公式求比值(2)三棱锥A′BC′D的体积等于正方体体积减去4个小三棱锥体积.
倍,根据三角形面积公式以及正方形面积公式求比值(2)三棱锥A′BC′D的体积等于正方体体积减去4个小三棱锥体积.
试题解析:(1)∵ABCDA′B′C′D′是正方体,∴六个面都是正方形,∴A′C′=A′B=A′D=BC′=BD=C′D=![]() a,∴S三棱锥=4×
a,∴S三棱锥=4×![]() ×(
×(![]() a)2=2
a)2=2![]() a2,S正方体=6a2,∴
a2,S正方体=6a2,∴![]() =
=![]() .
.
(2)显然,三棱锥A′ABD、C′BCD、DA′D′C′、BA′B′C′是完全一样的,
∴V三棱锥A′BC′D=V正方体-4V三棱锥A′ABD=a3-4×![]() ×
×![]() a2×a=
a2×a=![]() a3.
a3.

练习册系列答案
相关题目