题目内容
口袋中有n(n∈N＊)个白球，3个红球.依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球.记取球的次数为X,若P(X=2)=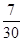
求：
（1）n的值；
（2）X的概率分布与数学期望.
（1）
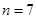；（2）X的数学期望是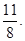
解析试题分析：（1）由题知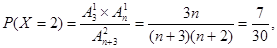
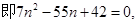
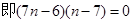，得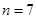；（2）由题知，X的可能取值为1，2，3，4，分别计算其概率，然后列分布列计算期望.
试题解析：（1）由题知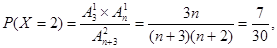
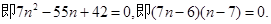
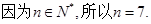5分
（2）由题知，X的可能取值为1，2，3，4，所以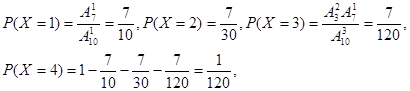
所以，X的概率分布表为
所以X 1 2 3 4 P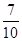 
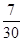
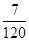
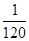
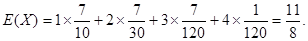
答：X的数学期望是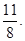 10分
考点：离散型随机变量的概率和期望、离散型随机变量的分布列、古典概型概率计算.
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关，随机抽取了55名市民，得到数据如下表：
| | 喜欢 | 不喜欢[来源:学科网ZXXK] | 合计 |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
(Ⅱ)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查，将这6位市民作为一个样本，从中任选2人，求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率．
下面的临界值表供参考：
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
，其中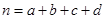
） 
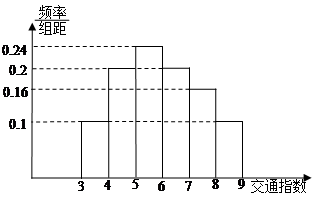
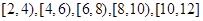五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在10米到12米之间．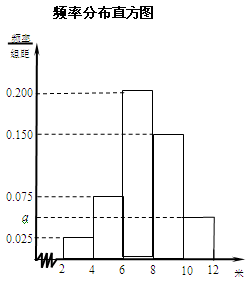
的值及参加“掷实心球”项目测试的人数；
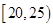，第2组
，第3组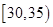
，第4组
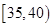，第5组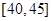
，得到的频率分布直方图如图所示.
，
，
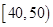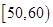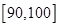后得到如图的频率分布直方图．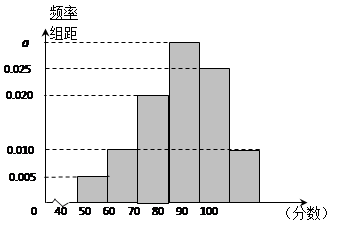
的值；