题目内容
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组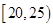 ,第2组
,第2组 ,第3组
,第3组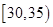 ,第4组
,第4组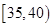 ,第5组
,第5组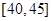 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
(1)3,2,1;(2)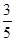 .
.
解析试题分析:(1)先由频率分布直方图得到第3,4,5组的概率,从而得到这三组中各组的人数以及三组总人数,所以易知这三组人数的比例关系,从而由分层抽样的定义确定在各组中应抽取多少人;(2)先确定在这6名志愿者中随机抽取2名志愿者共有多少种抽取方法,在确定第4组至少有一名志愿者被抽中时的抽取方法有多少种,用后者比前者即为所求.
试题解析:(1)第3组的人数为0.3×100=30, 第4组的人数为0.2×100=20, 第5组的人数为0.1×100=10. 3分
因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:第3组: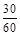 ×6="3;" 第4组:
×6="3;" 第4组: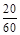 ×6="2;" 第5组:
×6="2;" 第5组: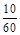 ×6=1.
×6=1.
所以应从第3,4,5组中分别抽取3人,2人,1人. 6分
(2)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,第5组的1名志愿者为C1.
则从6名志愿者中抽取2名志愿者有:
(A1,A2), (A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),
(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种. 8分
其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中的有:
(A1,B1), (A1,B2), (A2,B1), (A2,B2), (A3,B1), (A3,B2), (B1,B2), (B1,C1), (B2,C1),共有9种, 10分
所以第4组至少有一名志愿者被抽中的概率为 12分
12分
考点:1.分层抽样;2.频率分布直方图;3.随机事件的概率.

 习题精选系列答案
习题精选系列答案用分层抽样方法从高中三个年级的相关人员中抽取若干人组成研究小组,有关数据见下表:(单位:人)
| 年级 | 相关人数 | 抽取人数 |
| 高一 | 99 | 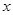 |
| 高二 | 27 | 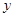 |
| 高三 | 18 | 2 |
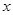 ,
,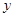 ;
;(Ⅱ)若从高二、高三年级抽取的人中选
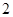 人,求这二人都来自高二年级的概率.
人,求这二人都来自高二年级的概率. 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | | | | b | | |
| 频率 | a | 0.25 | | | | |

(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格):
(2)从成绩在[100,130)范围内的学生中随机选4人,
设其中成绩在[100,110)内的人数为X,求X的分布列及数学期望.
从某学校高三年级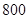 名学生中随机抽取
名学生中随机抽取 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 .第二组
.第二组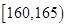 ; 第八组
; 第八组 ,下图是按上述分组方法得到的条形图.
,下图是按上述分组方法得到的条形图. 
(1)根据已知条件填写下面表格:
| 组 别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 样本数 | | | | | | | | |
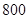 名学生中身高在
名学生中身高在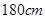 以上(含
以上(含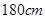 )的人数;
)的人数;(3)在样本中,若第二组有
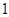 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有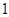 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少? 某校高三有甲、乙两个班,在某次数学测试中,每班各抽取5份试卷,所抽取的平均得分相等(测试满分为100分),成绩统计用茎叶图表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
(1)求
 ;
;(2)学校从甲班的5份试卷中任取两份作进一步分析,在抽取的两份样品中,求至多有一份得分在
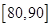 之间的概率.
之间的概率. 某高中在校学生2000人,高一年级与高二年级人数相同并且都比高三年级多1人,为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而且只参加其中一项,各年级参与项目人数情况如下表:
| | 高一年级 | 高二年级 | 高三年级 |
| 跑步 |  | 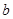 | 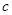 |
| 跳绳 |  |  | 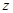 |
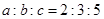 ,全校参与跳绳的人数占总人数的
,全校参与跳绳的人数占总人数的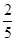 ,为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取 人.
,为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取 人. 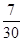 求:
求: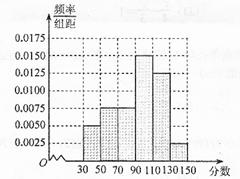
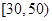 和
和 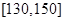 的学生中共抽取3人,该3人中成绩在
的学生中共抽取3人,该3人中成绩在