题目内容
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如图所示:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm的概率;
(3)从样本中身高在180~190cm的男生中任选2人,求至少有1人身高在185~190cm的概率.
(1)400(2)0.5(3)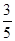
解析试题分析:(1)由频率分步直方图知样本中男生人数为2+5+13+14+2+4,全校以10%的比例对全校700名学生按性别进行抽样检查,知道每个个体被抽到的概率是0.1,得到分层抽样比例为10%估计全校男生人数.
(2)由图可知样本中身高在170~185cm之间的学生有14+13+4+3+1,样本容量为70,得到样本中学生身高在170~185cm之间的频率.用样本的频率来估计总体中学生身高在170~180cm之间的概率.
(3)由题意知本题是一个古典概型,通过列举法看出试验发生包含的所有事件数,再从这些事件中找出满足条件的事件数,根据古典概型公式,得到结果.
试题解析:(1)样本中男生人数为40,由分层抽样比例为10%,估计全校男生人数为400. 2分
(2)由统计图知,样本中身高在170~185 cm的学生有14+13+4+3+1=35(人),样本容量为70,所以样本中学生身高在170~185 cm之间的频率f=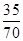 =0.5,故由f估计该校学生身高在170~185 cm的概率P1=0.5 6分
=0.5,故由f估计该校学生身高在170~185 cm的概率P1=0.5 6分
(3)样本中身高在180~185 cm的男生有4人,设其编号为①,②,③,④,
样本中身高在185~190 cm的男生有2人,设其编号为⑤,⑥,
从上述6人中任取2人的树状图为: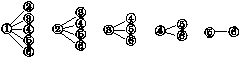
故从样本中身高在180~190cm之间的男生中任选2人得所有可能结果数为15 10分
至少有1人身高在185~190cm的可能结果数为9 12分
因此,所求概率P2=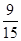 =
=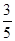 . 14分
. 14分
考点:1.频率分布直方图;2.频率与概率的关系;3.古典概型的求法

据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
某单位 名员工参加“社区低碳你我他”活动.他们的年龄在
名员工参加“社区低碳你我他”活动.他们的年龄在 岁至
岁至 岁
岁
之间.按年龄分组:第1组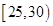 ,第
,第 组
组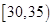 ,第3组
,第3组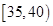 ,第
,第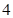 组
组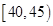 ,第
,第 组
组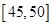 ,得到的频率分布直方图如图所示.下表是年龄的频率分布表.
,得到的频率分布直方图如图所示.下表是年龄的频率分布表.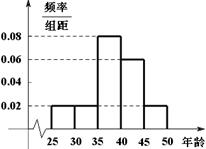
| 区间 | 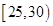 | 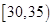 | 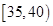 | 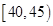 | 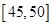 |
| 人数 |  |  |  | | |
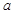 、
、 、
、 的值;
的值;(2)现要从年龄较小的第
 、
、 、
、 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取 人,则年龄在第
人,则年龄在第 、
、 、
、 组的人数分别
组的人数分别是多少?
(3)在(2)的条件下,从这
 人中随机抽取
人中随机抽取 人参加社区宣传交流活动,求恰有
人参加社区宣传交流活动,求恰有 人在第
人在第 组的概率.
组的概率. 某社团组织 名志愿者利用周末和节假日参加社会公益活动,活动内容是:1.到各社区宣传慰问,倡导文明新风;2.到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
名志愿者利用周末和节假日参加社会公益活动,活动内容是:1.到各社区宣传慰问,倡导文明新风;2.到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
| | 宣传慰问 | 义工 | 总计 |
 岁至 岁至 岁 岁 |  |  |  |
大于 岁 岁 |  | 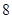 | 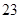 |
| 总计 |  |  |  |
 名,年龄大于
名,年龄大于 岁的应该抽取几名?
岁的应该抽取几名?(2)上述抽取的
 名志愿者中任取
名志愿者中任取 名,求选到的志愿者年龄大于
名,求选到的志愿者年龄大于 岁的人数的数学期望.
岁的人数的数学期望. 改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) | 1 | 2 | 3 | 4 | 5 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 |
 年多于10人的概率.
年多于10人的概率.(2)根据这
 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程 ,并计算第
,并计算第 年的估计值。
年的估计值。参考:用最小二乘法求线性回归方程系数公式

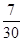 求:
求: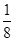 ,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),┅,第八组[190,195),右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组的频数均为4,第六组,第七组,第八组的频率依次构成等差数列。
,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),┅,第八组[190,195),右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组的频数均为4,第六组,第七组,第八组的频率依次构成等差数列。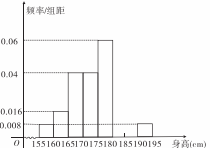
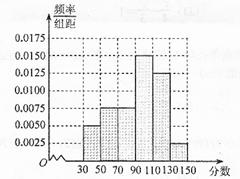
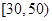 和
和 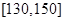 的学生中共抽取3人,该3人中成绩在
的学生中共抽取3人,该3人中成绩在
 是月用水量为[0,2)的家庭代表.
是月用水量为[0,2)的家庭代表. 是月用水量为[2,4]的家庭代表.若从这五位代表中任选两人参加水价听证会,请列举出所有不同的选法,并求家庭代表
是月用水量为[2,4]的家庭代表.若从这五位代表中任选两人参加水价听证会,请列举出所有不同的选法,并求家庭代表