题目内容
14．设集合A={x|-1≤x≤2}，B={y|y=2x-a，a∈R，x∈A}，C={z|z=x2，x∈A}，是否存在实数a，使得C⊆B？分析 假设存在符合题目要求的实数a．根据x∈A可以求得：C={z|0≤z≤4}、B={y|-2-a≤y≤4-a}．然后由限制性条件“C⊆B”列出关于a的不等式组并解答．
解答 解：假设存在符合题目要求的实数a．
当x∈A时，∵z=x2，
∴0≤z≤4，
∴C={z|0≤z≤4}．
∵y=2x-a，
∴-2-a≤y≤4-a，
∴B={y|-2-a≤y≤4-a}．
欲使C⊆B，则$\left\{\begin{array}{l}{-2-a≤0}\\{4-a≥4}\end{array}\right.$，
∴-2≤a≤0．
故存在实数a，且当-2≤a≤0时，C⊆B．
点评 本题考查了集合的包含关系判断及应用．解答该题需要掌握概念：如果集合A中的任意一个元素都是集合B的元素，那么集合A叫做集合B的子，表示为A⊆B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$均为单位向量，其夹角为θ，给出命题：p：|$\overrightarrow{a}$-$\overrightarrow{b}$|＞1；q：θ∈[$\frac{π}{2}$，$\frac{5π}{6}$），则p是q的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
5．通过市场调查，得到某产品的资金投入x（万元）与获得的利润y（万元）的数据，如下表所示：
参考公式：$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x\overline{y}}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$
（1）画出数据对应的散点图；
（2）根据上表提供的数据，用最小二乘法求线性回归直线方程$\widehat{y}$=bx+a；
（3）现投入资金10（万元），求估计获得的利润为多少万元．
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
（1）画出数据对应的散点图；
（2）根据上表提供的数据，用最小二乘法求线性回归直线方程$\widehat{y}$=bx+a；
（3）现投入资金10（万元），求估计获得的利润为多少万元．
2．
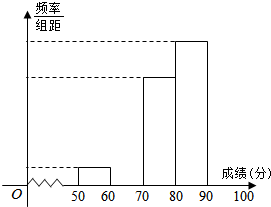青少年“心理健康”问题越来越引起社会关注，某校对高一600名学生进行了一次“心理健康”知识测试，并从中抽取了部分学生的成绩（得分取正整数，满分100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图．
（1）填写答题卡上频率分布表中的空格，并补全频率分布直方图；
（2）试估计该年段成绩在[70，90）段的有多少人？
（3）请你估算该年段的平均分．
青少年“心理健康”问题越来越引起社会关注，某校对高一600名学生进行了一次“心理健康”知识测试，并从中抽取了部分学生的成绩（得分取正整数，满分100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图．（1）填写答题卡上频率分布表中的空格，并补全频率分布直方图；
（2）试估计该年段成绩在[70，90）段的有多少人？
（3）请你估算该年段的平均分．
| 分组 | 频数 | 频率 |
| [50，60） | 2 | 0.04 |
| [60，70） | 8 | 0.16 |
| [70，80） | 10 | |
| [80，90） | ||
| [90，100] | 14 | 0.28 |
| 合计 | 1.00 |
19．
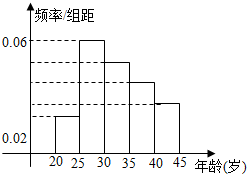某居民小区年龄在20岁到45岁的居民共有150人，如图是他们上网情况的频率分布直方图，现已知年龄在[30，35），[40，45]的人数分别是39、21人，则年龄在[35，40）的频数（ ）
某居民小区年龄在20岁到45岁的居民共有150人，如图是他们上网情况的频率分布直方图，现已知年龄在[30，35），[40，45]的人数分别是39、21人，则年龄在[35，40）的频数（ ）| A． | 6 | B． | 9 | C． | 30 | D． | 45 |
6．在中学综合素质评价某个维度的测评中，分“优秀、合格、尚待改进”三个等级进行学生互评，某校高二年级有男生500人，女生400人，为了了解性别对该维度测评结果的影响，采用分层抽样方法从高二年级抽取了45名学生的测评结果，并作出频数统计表如下：
表1：男生
表2：女生
（1）从表2的非优秀学生中随机选取2人交谈，求所选2人中恰有1人测评等级为合格的概率；
（2）由表中统计数据填写下边2×2列联表，并判断是否有90%的把握认为“测评结果优秀与性别有关”．
参考数据与公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$临界值表
表1：男生
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
（2）由表中统计数据填写下边2×2列联表，并判断是否有90%的把握认为“测评结果优秀与性别有关”．
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P（K2≥k0） | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |