Question

【题目】已知等差数列的公差，首项，且成等比数列.

（1）求数列的通项公式；

（2）求数列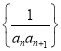的前n项和；

（3）比较与的大小.

Answer 1

【答案】（1）（2）（3）

【解析】

（1）由已知列式求得等差数列的公差，再由等差数列的通项公式求解；

（2）利用裂项相消法求数列{}的前n项和Pn；

（3）由，设f（n），分析可得当n≥3时，f（n+1）＞f（n）f（n）单调递增，由f（n）≥f（3），Pn，得f（n）＞Pn；再验证n＝1与n＝2时成立，可得Pn与的大小．

解：（1）由题意，，

即，解得d＝2．

∴an＝2n﹣1；

（2）

（3）由，

设f（n），则f（n+1）﹣f（n）．

当n≥3时，f（n+1）＞f（n），f（n）单调递增，

f（n）≥f（3），Pn，则f（n）＞Pn；

当n＝1时，f（1）＝2；

当n＝2时，f（2）＝1．

综上，Pn．