题目内容
【题目】已知经过点A(﹣4,0)的动直线l与抛物线G:x2=2py(p>0)相交于B、C,当直线l的斜率是 ![]() 时,
时, ![]() . (Ⅰ)求抛物线G的方程;
. (Ⅰ)求抛物线G的方程;
(Ⅱ)设线段BC的垂直平分线在y轴上的截距为b,求b的取值范围.
【答案】解:(Ⅰ)直线l的斜率是 ![]() 时,直线BC的方程为:x=2y﹣4,设B(x1 , y1),C(x2 , y2),
时,直线BC的方程为:x=2y﹣4,设B(x1 , y1),C(x2 , y2), 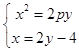 ,整理得:2y2﹣(8+p)y+8=0,
,整理得:2y2﹣(8+p)y+8=0,
由韦达定理可知:y1+y2= ![]() ,y1y2=4,
,y1y2=4,
由 ![]() .则y1=4y2 ,
.则y1=4y2 ,
由p>0,解得:y1=1,y2=4,
∴p=2,
∴抛物线G:x2=4y;
(Ⅱ)设l:y=k(x+4),BC中点坐标为(x0 , y0)
由 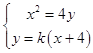 ,整理得:x2﹣4kx﹣16k=0,
,整理得:x2﹣4kx﹣16k=0,
∴由韦达定理可知:x1+x2=2k,则x0= ![]() =2k.则y0=k(x0+4)=2k2+4k,
=2k.则y0=k(x0+4)=2k2+4k,
∴BC的中垂线方程为y﹣(2k2+4k)=﹣ ![]() (x﹣2k),
(x﹣2k),
∴BC的中垂线在y轴上的截距为:b=2k2+4k+2=2(k+1)2 ,
对于方程由△=16k2+64k>0,解得:k>0或k<﹣4.
∴b的取值范围(2,+∞)
【解析】(1)设出B,C的坐标,利用点斜式求得直线l的方程,与抛物线方程联立消去x,利用韦达定理表示出x1+x2和x1x2 , 由 ![]() .根据求得y2=4y1 , 最后联立方程求得y1 , y2和p,则抛物线的方程可得.(2)设直线l的方程,AB中点坐标,把直线与抛物线方程联立,利用判别式求得k的范围,利用韦达定理表示出x1+x2 , 进而求得x0 , 利用直线方程求得y0 , 进而可表示出AB的中垂线的方程,求得其在y轴上的截距,根据k的范围确定b的范围.
.根据求得y2=4y1 , 最后联立方程求得y1 , y2和p,则抛物线的方程可得.(2)设直线l的方程,AB中点坐标,把直线与抛物线方程联立,利用判别式求得k的范围,利用韦达定理表示出x1+x2 , 进而求得x0 , 利用直线方程求得y0 , 进而可表示出AB的中垂线的方程,求得其在y轴上的截距,根据k的范围确定b的范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目