题目内容
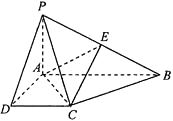
【题目】如图,在四棱锥 ![]() 中,
中, ![]() 底面
底面 ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证:平面 ![]() 平面
平面 ![]() ;
;
(Ⅱ)试在棱 ![]() 上确定一点
上确定一点 ![]() ,使截面
,使截面 ![]() 把该几何体分成的两部分
把该几何体分成的两部分 ![]() 与
与 ![]() 的体积比为
的体积比为 ![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,求二面角 ![]() 的余弦值.
的余弦值.
【答案】解:(Ⅰ)证明:∵ ![]() ,
,
∴ ![]() .
.
∵ ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() 平面
平面 ![]() .
.
∵ ![]() 平面
平面 ![]() ,
,
∴平面 ![]() 平面
平面 ![]() .
.
(Ⅱ)解:作 ![]() 于
于 ![]() 点,
点,
∵在 ![]() 中,
中, ![]() ,
,
∴ ![]() .
.
∴ ![]() 平面
平面 ![]() .
.
设 ![]() ,
,
则 ![]() .
.
![]() .
.
由 ![]() ,得
,得 ![]() ,解得
,解得 ![]() .
.
![]() ,故
,故 ![]() 为
为 ![]() 的中点.
的中点.
(Ⅲ)解:连接 ![]() 、
、 ![]() ,
, ![]() 与
与 ![]() 交于点
交于点 ![]() ,连接
,连接 ![]() ,
,

由(Ⅱ)可知 ![]() 平面
平面 ![]() ,所以
,所以 ![]() .
.
∵ ![]() 为正方形,
为正方形,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() 平面
平面 ![]() ,故
,故 ![]() .
.
∴ ![]() 是二面角
是二面角 ![]() 的平面角.
的平面角.
由 ![]() 平面
平面 ![]() ,可知平面
,可知平面 ![]() 平面
平面 ![]() .
.
∴二面角 ![]() 与二面角
与二面角 ![]() 互余.
互余.
设二面角 ![]() 的平面角为
的平面角为 ![]() ,则
,则 ![]() ,
,
在 ![]() 中,
中, ![]() ,
,
![]() ,
,
所以二面角 ![]() 的余弦值为
的余弦值为 ![]() .
.
【解析】(1)只需证明DC![]() AD,DC
AD,DC![]() PA即可;(2)过点E作EF
PA即可;(2)过点E作EF![]() AB,则EF
AB,则EF![]() PA,设EF=h,根据棱锥体积公式分别求出VP-ABCD和VE-ABC,则VPDCEA=VP-ABCD-VE-ABC,根据它们的体积之比可求出h 从而可确定点E的位置;(3)由题意可知二面角E—AC—B与二面角E—AC—P互余,因此二面角E—AC—B的正弦值即为二面角E—AC—P的余弦值.
PA,设EF=h,根据棱锥体积公式分别求出VP-ABCD和VE-ABC,则VPDCEA=VP-ABCD-VE-ABC,根据它们的体积之比可求出h 从而可确定点E的位置;(3)由题意可知二面角E—AC—B与二面角E—AC—P互余,因此二面角E—AC—B的正弦值即为二面角E—AC—P的余弦值.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.

练习册系列答案
相关题目