题目内容
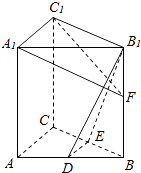
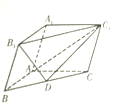
【题目】在四棱锥A﹣BCDE中,底面BCDE为平行四边形,平面ABE⊥平面BCDE,AB=AE,DB=DE,∠BAE=∠BDE=90°
(1)求异面直线AB与DE所成角的大小;
(2)求二面角B﹣AE﹣C的余弦值.
【答案】
(1)解:设BE的中点为O,连结AO,DO,
∵AB=AE,BO=OE,∴AO⊥BE,同理DO⊥BE,
又∵平面ABE⊥平面BCDE,
平面ABE∩平面BCDE=BE,
∴AO⊥平面BCDE,
由题意,BE2=2AB2=2DB2,
∴AB=BD=DE=AE,
设AB=1,以B为原点,以BC为x轴,BD为y轴,
建立如图所示的空间直角坐标系,
则B(0,0,0),C(1,0,0),D(0,1,0),
E(﹣1,1,0),A(﹣ ![]() ,
, ![]() ,
, ![]() ),
),
则 ![]() =(
=( ![]() ),
), ![]() =(﹣1,0,0),
=(﹣1,0,0),
∵cos< ![]() ,
, ![]() >=
>= 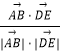 =
=  =﹣
=﹣ ![]() ,
,
∴ ![]() 与
与 ![]() 的夹角为120°,
的夹角为120°,
异面直线AB与DE所成角为60°.
(2)解:设平面ACE的法向量 ![]() =(x,y,z),
=(x,y,z),
![]() =(
=( ![]() ),
), ![]() =(﹣1,1,0),
=(﹣1,1,0),
则  ,取x=1,得
,取x=1,得 ![]() =(1,1,0),
=(1,1,0),
设平面ABE的法向量为 ![]() =(a,b,c),
=(a,b,c),
![]() =(
=( ![]() ),
), ![]() ,
,
则  ,取a=1,得
,取a=1,得 ![]() =(1,2,
=(1,2, ![]() ),
),
设二面角B﹣AE﹣C的平面角为θ,
cosθ=|cos< ![]() >|=
>|= ![]() =
= ![]() .
.
∴二面角B﹣AE﹣C的余弦值为 ![]() .
.

【解析】(1)设BE的中点为O,连结AO,DO,由已知得AO⊥BE,DO⊥BE,从而AO⊥平面BCDE,设AB=1,以B为原点,以BC为x轴,BD为y轴,建立空间直角坐标系,利用向量法能求出异面直线AB与DE所成角为60°.(2)求出平面ACE的法向量和平面ABE的法向量,由此利用向量法能求出二面角B﹣AE﹣C的余弦值.
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案