题目内容
【题目】如图,在四棱锥P﹣ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2 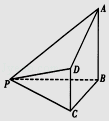
(1)证明:平面ABP⊥平面ADP;
(2)若直线PA与平面PCD所成角为α,求sinα的值.
【答案】
(1)证明:取AP的中点E,PB的中点F,连结DE,EF,CF,
则EF ![]() AB,
AB,
∵CD∥平面ABP,CD平面ABCD,平面ABCD∩平面ABP=AB,
∴CD∥AB,又CD= ![]() AB,
AB,
∴EF ![]() CD,
CD,
∴四边形DEFC是平行四边形,∴CF∥DE,
∵AB⊥平面BCP,CF平面BCP,
∴AB⊥CF,
∵BC=CP=BP,
∴CF⊥PB,又PB∩AB=B,
∴CF⊥平面ABP,
∴DE⊥平面ABP,又DE平面ADP,
∴平面ABP⊥平面ADP.
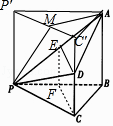
(2))解:过P作PP′∥AB,使得PP′=2,延长CD到C′,使得CC′=2,连结AC′,AP′,C′P′,
则直三棱柱PBC﹣P′AC′所有棱长均为2,
取P′C′的中点M,连结AM,则AM⊥平面PCC′P′,
∴∠APM是直线AP与平面PCD所成的角,即∠APM=α,
∵AM= ![]() =
= ![]() ,PA=
,PA= ![]() =2
=2 ![]() ,
,
∴sinα=sin∠APM= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)取AP的中点E,PB的中点F,连结DE,EF,CF,利用平行四边形得出DE∥CF,通过证明CF⊥平面APB得出DE⊥平面PAB,于是平面ABP⊥平面ADP;(2)将几何体补成直三棱柱,作出线面角,从而可求出sinα的值.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则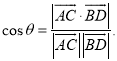 .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目



