题目内容
【题目】在平面直角坐标系xoy中,曲线C1的参数方程为 ![]() (α为参数),曲线C2的参数方程为
(α为参数),曲线C2的参数方程为 ![]() (β为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(β为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1和曲线C2的极坐标方程;
(2)已知射线l1:θ=α( ![]() <α<
<α< ![]() ),将射线l1顺时针方向旋转
),将射线l1顺时针方向旋转 ![]() 得到l2:θ=α﹣
得到l2:θ=α﹣ ![]() ,且射线l1与曲线C1交于两点,射线l2与曲线C2交于O,Q两点,求|OP||OQ|的最大值.
,且射线l1与曲线C1交于两点,射线l2与曲线C2交于O,Q两点,求|OP||OQ|的最大值.
【答案】
(1)解:∵曲线C1的参数方程为 ![]() (α为参数),
(α为参数),
∴曲线C1的直角坐标方程为(x﹣1)2+y2=1,
即x2+y2﹣2x=0,
∴曲线C1的极坐标方程为ρ2﹣2ρcosθ=0,即ρ=2cosθ.
∵曲线C2的参数方程为 ![]() (β为参数),
(β为参数),
∴曲线C2的普通方程x2+(y﹣1)2=1,即x2+y2﹣2y=0,
∴曲线C2的极坐标方程为ρ2﹣2ρsinθ=0,即ρ=2sinθ.
(2)解:设点P的极坐标为P(ρ1,α),即ρ1=2cosα,
设点Q的坐标为Q( ![]() ),即
),即 ![]() ,
,
∴|OP||OQ|=ρ1ρ2=2cos ![]() =4cosα(
=4cosα( ![]() sin
sin ![]() )
)
=2 ![]() sinαcosα﹣2cos2α=
sinαcosα﹣2cos2α= ![]() ﹣cos2α﹣1=2sin(2
﹣cos2α﹣1=2sin(2 ![]() )﹣1,
)﹣1,
∵α∈( ![]() ),∴
),∴ ![]() ∈(
∈( ![]() ),
),
当2 ![]() =
= ![]() ,即
,即 ![]() 时,|OP||OQ|取最大值1.
时,|OP||OQ|取最大值1.
【解析】(1)由曲线C1的参数方程能求出曲线C1的直角坐标方程,从而能求出曲线C1的极坐标方程.由曲线C2的参数方程能求出曲线C2的直角坐标方程,从而能求出曲线C2的极坐标方程.(2)设点P的极坐标为P(ρ1 , α),即ρ1=2cosα,设点Q的坐标为Q( ![]() ),即
),即 ![]() ,mh|OP||OQ|=ρ1ρ2=2cos
,mh|OP||OQ|=ρ1ρ2=2cos ![]() =2sin(2
=2sin(2 ![]() )﹣1,能求出|OP||OQ|的最大值.
)﹣1,能求出|OP||OQ|的最大值.

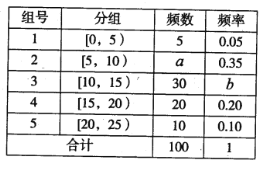
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
【题目】近几年,京津冀等地数城市指数“爆表”,尤其2015年污染最重.为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于的线性回归方程;
(2)(ⅰ)利用(1)所求的回归方程,预测该市车流量为8万辆时![]() 的浓度;
的浓度;
(ⅱ)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)