Question

【题目】选修4﹣4：坐标系与参数方程
在直角坐标xOy中，圆C1：x2+y2=4，圆C2：（x﹣2）2+y2=4．
（1）在以O为极点，x轴正半轴为极轴的极坐标系中，分别写出圆C1 ， C2的极坐标方程，并求出圆C1 ， C2的交点坐标（用极坐标表示）；
（2）求圆C1与C2的公共弦的参数方程．

Answer 1

【答案】
（1）

解：由 ，x2+y2=ρ2，

可知圆 ，的极坐标方程为ρ=2，

圆 ，即 的极坐标方程为ρ=4cosθ，

解 得：ρ=2， ，

故圆C1，C2的交点坐标（2， ），（2， ）．

（2）

解法一：由 得圆C1，C2的交点的直角坐标（1， ），（1，- ）．

故圆C1，C2的公共弦的参数方程为

（或圆C1，C2的公共弦的参数方程为 ）

解法二：将x=1代入 得ρcosθ=1

从而 于

是圆C1，C2的公共弦的参数方程为

【解析】（1）利用 ，以及x2+y2=ρ2 ， 直接写出圆C1 ， C2的极坐标方程，求出圆C1 ， C2的交点极坐标，然后求出直角坐标（用坐标表示）；（2）解法一：求出两个圆的直角坐标，直接写出圆C1与C2的公共弦的参数方程．
解法二：利用直角坐标与极坐标的关系求出 ，然后求出圆C1与C2的公共弦的参数方程．
【考点精析】本题主要考查了直线的参数方程的相关知识点，需要掌握经过点，倾斜角为的直线的参数方程可表示为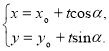（为参数）才能正确解答此题．