题目内容
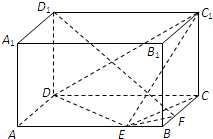 如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2.E、F分别是线段AB、BC上的点,且EB=FB=1.
如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2.E、F分别是线段AB、BC上的点,且EB=FB=1.(1)求直线EC1与FD1所成角的余弦值;
(2)求二面角C-DE-C1的平面角的正切值.
分析:(1)以A为原点,
,
,
分别为x轴,y轴,z轴的正向建立空间直角坐标系A-xyz,写出要用的点的坐标,把两条直线对应的点的坐标写出来,根据两个向量之间的夹角表示出异面直线的夹角.
(2)设出平面的法向量的坐标,根据法向量与平面上的向量垂直,利用数量积表示出两个向量的坐标之间的关系,求出平面的一个法向量,根据两个向量之间的夹角求出结果.
| AB |
| AD |
| AA1 |
(2)设出平面的法向量的坐标,根据法向量与平面上的向量垂直,利用数量积表示出两个向量的坐标之间的关系,求出平面的一个法向量,根据两个向量之间的夹角求出结果.
解答: 解:以A为原点,
解:以A为原点,
,
,
分别为x轴,y轴,z轴的正向建立空间直角坐标系A-xyz,则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2).
于是,
=(3,-3,0),
=(1,3,2),
=(-4,2,2).
(1)设EC1与FD1所成角为β,则cosβ=|
|=|
|=
.
(2)设向量
=(x,y,z)与平面C1DE垂直,则有
?
?x=y=-
z.
∴
=(-
,-
,z)=
(-1,-1,2),其中z>0.
取n0=(-1,-1,2),则是一个与平面C1DE垂直的向量.
∵向量
=(0,0,2)与平面CDE垂直,
∴n0与
所成的角θ为二面角C-DE-C1的平面角.
∵cosθ=
=
=
,
∴tanθ=
.
 解:以A为原点,
解:以A为原点,| AB |
| AD |
| AA1 |
于是,
| DE |
| EC1 |
| FD1 |
(1)设EC1与FD1所成角为β,则cosβ=|
| ||||
|
|
| 1×(-4)+3×2+2×2 | ||||
|
| ||
| 14 |
(2)设向量
| n |
|
|
| 1 |
| 2 |
∴
| n |
| z |
| 2 |
| z |
| 2 |
| z |
| 2 |
取n0=(-1,-1,2),则是一个与平面C1DE垂直的向量.
∵向量
| AA1 |
∴n0与
| AA1 |
∵cosθ=
n0•
| ||
|n0|×|
|
| -1×0-1×0+2×2 | ||||
|
| ||
| 3 |
∴tanθ=
| ||
| 2 |
点评:本题考查用空间向量求平面间的夹角,本题解题的关键是建立适当的坐标系,写出要用的空间向量,把立体几何的理论推导变成数字的运算,这样降低了题目的难度.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.