题目内容
10.已知函数f(x)=$\frac{1-lnx}{x^2}$.(Ⅰ)求函数f(x)的零点及单调区间;
(Ⅱ)求证:曲线y=$\frac{lnx}{x}$存在斜率为6的切线,且切点的纵坐标y0<-1.
分析 (Ⅰ)令f(x)=0,求出函数的零点,求出函数的导数,从而求出函数的单调区间;
(Ⅱ)令$g(x)=\frac{lnx}{x}$,求出函数的导数,结合函数的单调性得到得:$ln{x_0}=1-6x_0^2$,从而证出结论.
解答 解:(Ⅰ)令f(x)=0,得x=e.故f(x)的零点为e,
$f'(x)=\frac{{(-\frac{1}{x})•{x^2}-(1-lnx)•2x}}{{{{({x^2})}^2}}}=\frac{2lnx-3}{x^3}$(x>0).
令 f′(x)=0,解得 $x={e^{\frac{3}{2}}}$.
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (0,${e}^{\frac{3}{2}}$) | ${e}^{\frac{3}{2}}$ | (${e}^{\frac{3}{2}}$,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 递增 |
(Ⅱ)令$g(x)=\frac{lnx}{x}$.则$g'(x)=\frac{{\frac{1}{x}•x-1•lnx}}{x^2}=\frac{1-lnx}{x^2}=f(x)$,
因为 $f(\frac{1}{2})=4+4ln2>4+4×\frac{1}{2}=6$,f(e)=0,且由(Ⅰ)得,f(x)在(0,e)内是减函数,
所以 存在唯一的${x_0}∈(\frac{1}{2},e)$,使得g′(x0)=f(x0)=6.
当x∈[e,+∞)时,f(x)≤0.
所以 曲线$y=\frac{lnx}{x}$存在以(x0,g(x0))为切点,斜率为6的切线.
由$g'({x_0})=\frac{{1-ln{x_0}}}{x_0^2}=6$得:$ln{x_0}=1-6x_0^2$.
所以 $g({x_0})=\frac{{ln{x_0}}}{x_0}=\frac{1-6x_0^2}{x_0}=\frac{1}{x_0}-6{x_0}$.
因为 ${x_0}>\frac{1}{2}$,所以 $\frac{1}{x_0}<2$,-6x0<-3.
所以 y0=g(x0)<-1.
点评 本题考查了函数的单调性,函数的零点问题,考查导数的应用,考查曲线的切线问题,是一道中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
5.已知命题p,q,那么“p∧q为真命题”是“p∨q为真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知点A(a,a)(a≠0),B(1,0),O为坐标原点.若点C在直线OA上,且BC与OA垂直,则点C的坐标是( )
| A. | $(\frac{1}{2},\;-\frac{1}{2})$ | B. | $(\frac{a}{2},\;-\frac{a}{2})$ | C. | $(\frac{a}{2},\;\frac{a}{2})$ | D. | $(\frac{1}{2},\;\frac{1}{2})$ |
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左右焦点分别为F1(-c,0),F2(c,0),若双曲线右支上存在异于顶点的点P满足c•sin∠PF1F2=3a•sin∠PF2F1,则双曲线的离心率的取值范围是( )
| A. | $(1,1+\sqrt{7})$ | B. | $(1,2+\sqrt{7})$ | C. | $(3,1+\sqrt{7})$ | D. | (3,2+$\sqrt{7}$) |
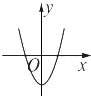 B、
B、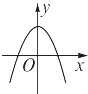 C、
C、 D、
D、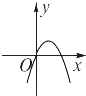
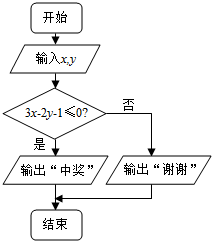 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、200人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取10人在前排就坐,其中高二代表队有5人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、200人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取10人在前排就坐,其中高二代表队有5人.