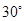题目内容
如图,在长方体 中,
中, 点
点 在棱
在棱 上.
上.

(1)求异面直线 与
与 所成的角;
所成的角;
(2)若二面角 的大小为
的大小为 ,求点
,求点 到面
到面 的距离.
的距离.
 中,
中, 点
点 在棱
在棱 上.
上.
(1)求异面直线
 与
与 所成的角;
所成的角;(2)若二面角
 的大小为
的大小为 ,求点
,求点 到面
到面 的距离.
的距离.(1)对于异面直线的所成的角,一般采用平移法,平移到一个三角形中,借助于余弦定理求解。
(2)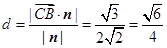
(2)
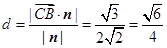
试题分析:解法一:(1)连结
 .由
.由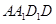 是正方形知
是正方形知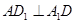 .
.∵
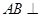 平面
平面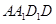 ,
,∴
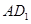 是
是 在平面
在平面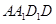 内的射影.
内的射影.根据三垂线定理得
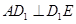 ,
,则异面直线
 与
与 所成的角为
所成的角为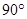 . 5分
. 5分(2)作
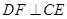 ,垂足为
,垂足为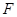 ,连结
,连结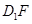 ,则
,则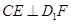 .
.所以
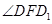 为二面角
为二面角 的平面角,
的平面角,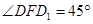 .于是
.于是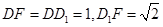 ,
,易得
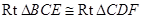 ,所以
,所以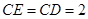 ,又
,又 ,所以
,所以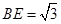 .
.设点
 到平面
到平面 的距离为
的距离为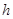 ,则由于
,则由于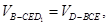 即
即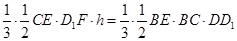 ,
,因此有
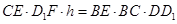 ,即
,即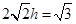 ,∴
,∴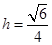 .…………12分
.…………12分解法二:如图,分别以
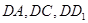 为
为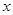 轴,
轴,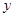 轴,
轴,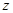 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.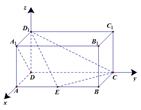
(1)由
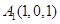 ,得
,得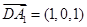 ,
,设
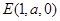 ,又
,又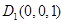 ,则
,则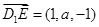 .
.∵
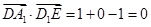 ∴
∴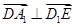 ,则异面直线
,则异面直线 与
与 所成的角为
所成的角为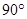 . 5分
. 5分(2)
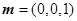 为面
为面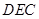 的法向量,设
的法向量,设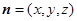 为面
为面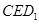 的法向量,则
的法向量,则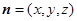
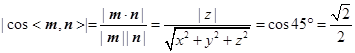 ,
,∴
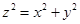 . ①
. ①由
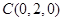 ,得
,得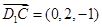 ,则
,则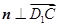 ,即
,即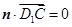 ,∴
,∴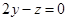
②由①、②,可取
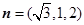 ,又
,又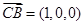 ,
,所以点
 到平面
到平面 的距离
的距离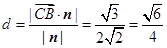 . 12分
. 12分点评:考查了异面直线所成的角以及点到面的距离的求解,属于基础题。

练习册系列答案
相关题目
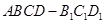 中,四边形
中,四边形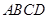 为菱形,
为菱形,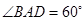 ,
,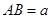 ,面
,面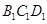 ∥面
∥面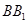 、
、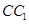 、
、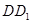 都垂直于面
都垂直于面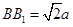 ,
,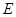 为
为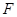 为
为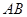 的中点.
的中点.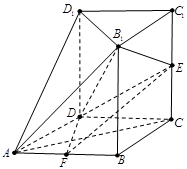
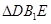 为等腰直角三角形;
为等腰直角三角形;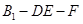 的大小.
的大小.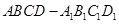 ,
,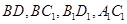 分别为各个面的对角线;
分别为各个面的对角线;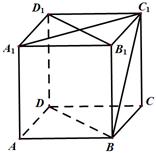
 ;
; 所成的角.
所成的角. 中,
中, 则
则 所成的角的大小是
所成的角的大小是



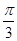 ,π);
,π);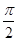 ;
;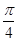 的直线有3条;
的直线有3条;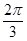 ,则过点N与平面PAC和平面PAB都成
,则过点N与平面PAC和平面PAB都成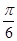 的直线有3条.
的直线有3条. 中,
中, ,
, ,则异面直线
,则异面直线 与
与 所成的角为 ( )
所成的角为 ( )




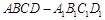 中,
中,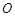 为
为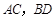 的交点,则
的交点,则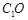 与
与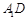 所成角的( )
所成角的( )



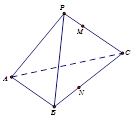
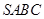 中,各边及对角线长都相等,若
中,各边及对角线长都相等,若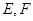 分别为
分别为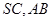 的中点,那么异面直线
的中点,那么异面直线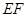 与
与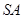 所成的角等于( )
所成的角等于( )