题目内容
【题目】如图，菱形
的对角线
与
交于点O，
，点
分别在
上，
，
交于点
. 将
沿折到△
的位置，
.
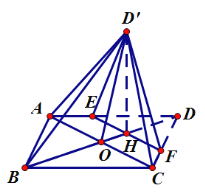
（1）证明：
平面；
（2）求二面角
的余弦值.
【答案】（1）详见解析；（2）
.
【解析】
（1）根据折叠前后关系可证
，再用勾股定理证
，即可证得结论；
（2）建立空间坐标系，求出平面
的法向量，找出平面
的法向量，即可求出结果.
（I）由已知得
，
，
又由
得
，故
.
因此
，从而
由
,
，
得
.
由
得
.
所以
，
.
于是
，故.
又
，而
，
所以
平面
.
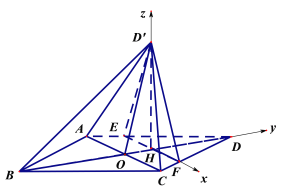
（II）如图，以
为坐标原点，
的方向为
轴的正方向，
建立空间直角坐标系
，则
，
，
，
，
，
，
.
设
是平面的法向量，
则
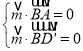，即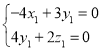
，
所以可以取
因菱形ABCD中有
，
又由（1）知
所以
是平面的法向量，
设二面角
为
，由于为锐角，
于是
.
因此二面角
的余弦值是.
练习册系列答案
相关题目
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店，为合理安排各地区加盟店的个数，先在其中5个地区试点，得到试点地区加盟店个数分别为1，2，3，4，5时，单店日平均营业额
（万元）的数据如下：
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
（1）求单店日平均营业额（万元）与所在地区加盟店个数
（个）的线性回归方程；
（2）根据试点调研结果，为保证规模和效益，在其他5个地区，该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元，求一个地区开设加盟店个数
的所有可能取值；
（3）小赵与小王都准备加入该公司的加盟店，根据公司规定，他们只能分别从其他五个地区（加盟店都不少于2个）中随机选一个地区加入，求他们选取的地区相同的概率.
（参考数据及公式：
，
，线性回归方程
，其中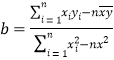
，
.）
