��Ŀ����
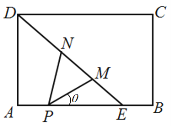
����Ŀ����2017����һģ����ͼ������ABCD��һ����ʷ����չ�����ĸ���ͼ����E��AB�ϣ�������BCDE�����ڲ�չʾ���DE�Dz���Ļǽ���ο�ֻ����![]() ADE�����ڲιۣ���AE�ϵ�P����װһ����ת�ļ������ͷ��
ADE�����ڲιۣ���AE�ϵ�P����װһ����ת�ļ������ͷ��![]() Ϊ��ؽǣ�����M��N���߶�DE�����˵㣩�ϣ��ҵ�M�ڵ�N�����·�.��������֪��AD=6�ף�AE=6�ף�AP=2�ף�
Ϊ��ؽǣ�����M��N���߶�DE�����˵㣩�ϣ��ҵ�M�ڵ�N�����·�.��������֪��AD=6�ף�AE=6�ף�AP=2�ף�![]() .��
.��![]() �����ȣ����������ͷ�Ŀ�������
�����ȣ����������ͷ�Ŀ�������![]() PMN�����ΪSƽ���ף�
PMN�����ΪSƽ���ף�
��1����S����![]() �ĺ�����ϵʽ����д��
�ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ�����ο����ݣ�
��ȡֵ��Χ�����ο����ݣ�![]() ��
��
��2����![]() ����Сֵ.
����Сֵ.
���𰸡�������
���������ŷ���һ����![]() PME�У�
PME�У�![]() ��PE=AE-AP=4�ף�
��PE=AE-AP=4�ף�![]() ��
��![]() ��
��
�����Ҷ�����![]() ��
��
����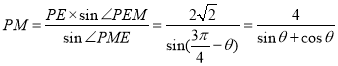 ��---------------------2��
��---------------------2��
ͬ����![]() PNE�У������Ҷ�����
PNE�У������Ҷ�����![]() ��
��
����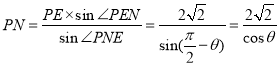 ��---------------------4��
��---------------------4��
����![]() PMN�����S
PMN�����S![]()
![]()
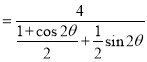
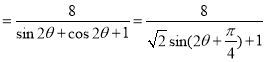 ��--------------------8��
��--------------------8��
��M��E�غ�ʱ��![]() ����N��D�غ�ʱ��
����N��D�غ�ʱ��![]() ,��
,��![]() ��
��![]() ��
��
����![]() .
.
���Ͽɵã�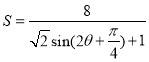 ,
,![]() .---------------------10��
.---------------------10��
����������![]() PME��
PME�У�![]() ��PE=AE-AP=4�ף�
��PE=AE-AP=4�ף�![]() ��
��![]() �������Ҷ�����֪��
�������Ҷ�����֪��![]() ��
��
����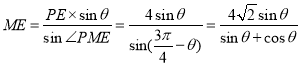 ��---------------------2��
��---------------------2��
��![]() PNE�У������Ҷ�����֪��
PNE�У������Ҷ�����֪��![]() ��
��
����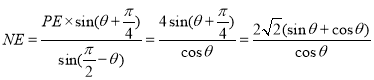 ��---------------------4��
��---------------------4��
����![]() ,
,
�ֵ�P��DE�ľ���Ϊ![]() ��---------------------6��
��---------------------6��
����![]() PMN�����S=
PMN�����S=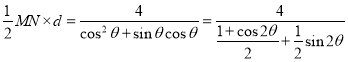
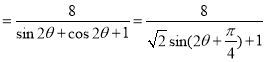 ��---------------------8��
��---------------------8��
��M��E�غ�ʱ��![]() ����N��D�غ�ʱ��
����N��D�غ�ʱ��![]() ,��
,��![]() ��
��![]() ��
��
����![]() .
.
���Ͽɵã�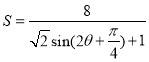 ,
,![]() .---------------------10��
.---------------------10��
�Ƶ�![]() ��
��![]() ʱ��
ʱ��![]() ȡ����СֵΪ
ȡ����СֵΪ![]() .---------13��
.---------13��
������������![]() PMN�������СֵΪ
PMN�������СֵΪ![]() ƽ����.---------------------14��
ƽ����.---------------------14��

����Ŀ����ij�β����У���6λͬѧ��ƽ���ɼ�Ϊ75�֣���xn��ʾ���Ϊn��n=1��2������6����ͬѧ���óɼ�����ǰ5λͬѧ�ijɼ����£�
���n | 1 | 2 | 3 | 4 | 5 |
�ɼ�xn | 70 | 76 | 72 | 70 | 72 |
��1�����6λͬѧ�ijɼ�x6 �� ����6λͬѧ�ɼ��ı���s��
��2����ǰ5λͬѧ�У������ѡ2λͬѧ����ǡ��1λͬѧ�ɼ������䣨68��75���еĸ��ʣ�