题目内容
【题目】已知
，
是椭圆
的左、右焦点，椭圆
过点
.
（1）求椭圆的方程；
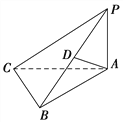
（2）过点
的直线
（不过坐标原点）与椭圆交于
，
两点，且点在
轴上方，点在轴下方，若
，求直线的斜率.
【答案】（1）
（2）
【解析】
(1) 由条件知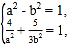
从而解得
，即可得到椭圆
的方程；
（2）设
，
，则
，
，设直线
的方程为
，代入椭圆的方程消去
，得
，由韦达定理及
可建立关于未知量的方程，解之即可.
（1）由条件知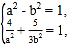解得
因此椭圆的方程为.
（2）解法一：设，，则，，
设直线的方程为，
代入椭圆的方程消去，得，
由韦达定理得
，
，
由知
，即
，
带入上式得
，
所以
，解得
，
结合图形知
，故直线的斜率为.
解法二：设，，则，，
设直线的方程为，
代入椭圆的方程消去，得，
因此
，
，
由知，
代入上式得
，
解得，
结合图形知，故直线的斜率为.
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战，某帮扶单位为帮助定点扶贫村扶贫. 此帮扶单位为了了解某地区贫困户对其所提供的帮扶的满意度，随机调查了40个贫困户，得到贫困户的满意度评分如下：
贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系统抽样法从40名贫困户中抽取容量为10的样本，且在第一分段里随机抽到的评分数据为92.
（1）请你列出抽到的10个样本的评分数据；
（2）计算所抽到的10个样本的均值
和方差
；
（3）在（2）条件下，若贫困户的满意度评分在
之间，则满意度等级为“
级”.运用样本估计总体的思想，现从（1）中抽到的10个样本的满意度为“
级”贫困户中随机地抽取2户，求所抽到2户的满意度均评分均“超过80”的概率.
（参考数据：
）