题目内容
【题目】抛物线![]() :
:![]() ,直线
,直线![]() 的斜率为2.
的斜率为2.
(Ⅰ)若![]() 与
与![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 相交于
相交于![]() ,
,![]() ,线段
,线段![]() 的中垂线交
的中垂线交![]() 于
于![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 与抛物线
与抛物线![]() 的方程联立,利用
的方程联立,利用![]() 求出
求出![]() 的值,从而得出直线
的值,从而得出直线![]() 的方程;
的方程;
(2)设点![]() 、
、![]() 、
、![]() 、
、![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立,由
的方程联立,由![]() 得出
得出![]() 的范围,并列出韦达定理,求出
的范围,并列出韦达定理,求出![]() 并求出线段
并求出线段![]() 的中点坐标,然后得出线段
的中点坐标,然后得出线段![]() 中垂线的方程
中垂线的方程![]() ,将直线
,将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立,列出韦达定理并求出
的方程联立,列出韦达定理并求出![]() ,然后得出
,然后得出![]() 的表达式,结合不等式的性质求出这个代数式的取值范围.
的表达式,结合不等式的性质求出这个代数式的取值范围.
解:(1)设直线![]() 的方程为
的方程为![]() ,联立直线
,联立直线![]() 抛物线
抛物线![]() 的方程
的方程![]() ,得
,得![]() ,
,
![]() ,所以,
,所以,![]() ,
,
因此,直线![]() 的方程为
的方程为![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() 、
、![]() 、
、![]() ,
,
联立直线![]() 与抛物线
与抛物线![]() 的方程
的方程![]() ,得
,得![]() ,
,![]() ,所以,
,所以,![]() .
.
由韦达定理得![]() ,
,![]() .
.
所以,![]() ,
,
因为线段![]() 的中点为
的中点为![]() ,所以,直线
,所以,直线![]() 的方程为
的方程为![]() ,
,
由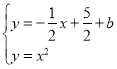 ,得
,得![]() ,由韦达定理得
,由韦达定理得![]() ,
,![]() ,
,
所以,![]() ,
,
所以,![]() ,
,
所以,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


