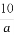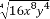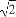题目内容
设定义在R上的函数f(x)同时满足以下条件:①f(x)+f(-x)=0;②f(x)=f(x+2);③当0≤x≤1时,f(x)=2x-1,则f(
)+f(1)+f(
)+f(2)+f(
)
= .
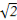
【解析】【思路点拨】根据条件先探究函数的奇偶性、周期性,再将所求函数值转化为已知函数值求解.
解:依题意知:函数f(x)为奇函数且周期为2,
∴f(
)+f(1)+f(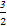
)+f(2)+f(
)
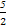=f()+f(1)+f(-)+f(0)+f()
=f()+f(1)-f()+f(0)+f()
=f()+f(1)+f(0)
=
-1+21-1+20-1
=.
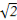练习册系列答案
名校课堂系列答案
相关题目
