题目内容
11.(1)若f(x)=cos2(2x+$\frac{π}{6}$),则f′(x)=-2sin(4x+$\frac{π}{3}$);(2)若f(x)=ln$\sqrt{\frac{1-x}{1+x}}$,则f′(x)=$\frac{1}{{x}^{2}-1}$.
分析 根据函数的导数公式进行计算即可.
解答 解:(1)∵f(x)=cos2(2x+$\frac{π}{6}$),
∴f′(x)=2cos(2x+$\frac{π}{6}$)(-sin(2x+$\frac{π}{6}$))×2=-2sin(4x+$\frac{π}{3}$).
(2)∵f(x)=ln$\sqrt{\frac{1-x}{1+x}}$=$\frac{1}{2}$ln$\frac{1-x}{1+x}$=$\frac{1}{2}$ln(1-x)-$\frac{1}{2}$ln(1+x),
∴f′(x)=$\frac{1}{2}•\frac{1}{1-x}×(-1)$-$\frac{1}{2}•\frac{1}{1+x}$=$\frac{1}{2}•\frac{1}{x-1}$-$\frac{1}{2}•\frac{1}{1+x}$=$\frac{1}{(x+1)(x-1)}$=$\frac{1}{{x}^{2}-1}$,
故答案为:-2sin(4x+$\frac{π}{3}$),$\frac{1}{{x}^{2}-1}$
点评 本题主要考查函数的导数的计算,根据复合函数的导数公式是解决本题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
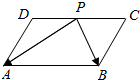 如图,在平行四边形ABCD中,AB=6,AD=4.点P是DC边的中点,则$\overrightarrow{PA}•\overrightarrow{PB}$的值为7.
如图,在平行四边形ABCD中,AB=6,AD=4.点P是DC边的中点,则$\overrightarrow{PA}•\overrightarrow{PB}$的值为7. 如图,在正棱柱ABC-A1B1C1中,E,F分别为线段AA1,C1B的中点,求证:EF∥平面ABC.
如图,在正棱柱ABC-A1B1C1中,E,F分别为线段AA1,C1B的中点,求证:EF∥平面ABC.