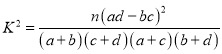题目内容
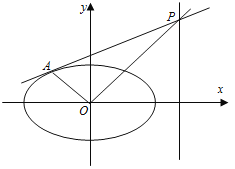
【题目】已知椭圆![]() ,点
,点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作椭圆的切线
作椭圆的切线![]() ,切点为
,切点为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)若切线![]() 的斜率为1,求点
的斜率为1,求点![]() 的坐标;
的坐标;
(2)求![]() 的面积的最小值,并求出此时
的面积的最小值,并求出此时![]() 的斜率.
的斜率.
【答案】(1)![]() 或
或![]() (2)
(2)![]() ,斜率为
,斜率为![]()
【解析】
(1)设切线![]() ,将直线与椭圆方程联立消
,将直线与椭圆方程联立消![]() ,得到关于
,得到关于![]() 的一元二次方程,
的一元二次方程,![]() 即可求解.
即可求解.
(2)设切线![]() ,将直线与椭圆方程联立消
,将直线与椭圆方程联立消![]() ,
,![]() ,得到
,得到![]()
求得![]() ,由
,由![]() ,令
,令![]() ,则
,则![]() ,代入
,代入![]() ,
,![]() ,即可求解;另解:设
,即可求解;另解:设![]() ,可得
,可得![]() ,由
,由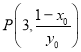 ,根据
,根据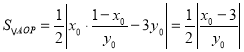 ,设直线
,设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,得
,得 ,当
,当![]() 与椭圆相切时,
与椭圆相切时,![]() 最大,进而可求解.
最大,进而可求解.
解:(1)设切线![]()
![]() 得到
得到![]()
![]() ,得到
,得到![]() ,所以
,所以![]()
所以![]() 或
或![]()
(2)设切线![]()
![]() 得到
得到![]()
![]() ,得到
,得到![]()
∴![]()
∴![]()
令![]() ,则
,则![]() ,代入
,代入![]() ,得到
,得到![]()
![]() ,得到
,得到![]() ,所以
,所以![]()
所以![]()
此时![]() .
.
另解:设![]() ,则
,则![]()
所以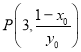
∴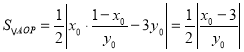
设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,则∴
,则∴ ,
,
当![]() 与椭圆相切时,
与椭圆相切时,![]() 最大,即
最大,即![]() 的面积最小
的面积最小
所以![]() ,此时
,此时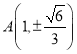 ,所以
,所以![]()
∴![]()

 名校课堂系列答案
名校课堂系列答案【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数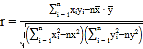 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: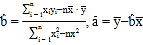 .
.
【题目】为了检验“喜欢玩手机游戏与认为作业多”是否有关系,某班主任对班级的30名学生进行了调查,得到一个![]() 列联表:
列联表:
认为作业多 | 认为作业不多 | 合计 | |
喜欢玩手机游戏 | 18 | 2 | |
不喜欢玩手机游戏 | 6 | ||
合计 | 30 |
(1)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
(2)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(3)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
参考公式及参考数据:独立性检验概率表
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
计算公式: