题目内容
【题目】为了检验“喜欢玩手机游戏与认为作业多”是否有关系,某班主任对班级的30名学生进行了调查,得到一个![]() 列联表:
列联表:
认为作业多 | 认为作业不多 | 合计 | |
喜欢玩手机游戏 | 18 | 2 | |
不喜欢玩手机游戏 | 6 | ||
合计 | 30 |
(1)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
(2)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(3)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
参考公式及参考数据:独立性检验概率表
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
计算公式: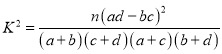
【答案】(1)理由见解析;(2)能;(3)![]() .
.
【解析】
(1)根据已知完成2×2列联表;(2)先求出![]() ,利用独立性检验得解;(3)利用互斥事件的概率和公式求解即可.
,利用独立性检验得解;(3)利用互斥事件的概率和公式求解即可.
(1)
认为作业多 | 认为作业不多 | 合计 | |
喜欢玩手机游戏 | 18 | 2 | 20 |
不喜欢玩手机游戏 | 4 | 6 | 10 |
合计 | 22 | 8 | 30 |
(2)假设“喜欢玩手机游戏”与“认为作业多” 无关,
则由上表数据得:  ,
,
又![]() ,有
,有![]() .
.
故在犯错误的概率不超过0.005的前提下,认为“喜欢玩手机游戏”与“认为作业多”有关.
(3)设认为作业不多的人数为![]() ,则所求概率为
,则所求概率为
![]() .
.

练习册系列答案
相关题目