题目内容
(本小题14分)
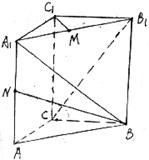
如图2,在四面体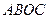 中,
中,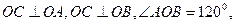 且
且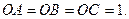
(1)设 为
为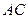 的中点,证明:在
的中点,证明:在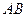 上存在一点
上存在一点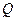 ,使
,使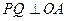 ,并计算
,并计算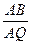 的值;
的值;
(2)求二面角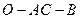 的平面角的余弦值.
的平面角的余弦值. 
如图2,在四面体
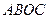 中,
中,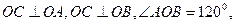 且
且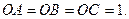
(1)设
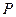 为
为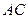 的中点,证明:在
的中点,证明:在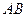 上存在一点
上存在一点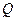 ,使
,使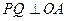 ,并计算
,并计算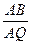 的值;
的值;(2)求二面角
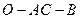 的平面角的余弦值.
的平面角的余弦值. 
解法一:(1)在平面 内作
内作 交
交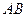 于
于 ,连接
,连接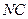 .…………1分
.…………1分

又 ,
, 
 ,
,  。
。

取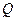 为
为 的中点,则
的中点,则
 …………4分
…………4分
在等腰 中,
中, ,
, 
在 中,
中, ,
, ……4分
……4分
在 中,
中, ,
,  …5分
…5分
 …………8分
…………8分
(2)连接 ,
,
由 ,
,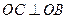 知:
知: .
.
又 ,
,
又由 ,
, .
.
又
 ,
,
又
 是
是 的中点,
的中点,

 ,
,
 ,
, ,
,
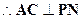
 为二面角
为二面角 的平面角 …………10分
的平面角 …………10分
在等腰 中,
中, ,
,
在 中,
中, ,
,
 在
在 中,
中,  . …………12分
. …………12分
 …………14分
…………14分

解法二:在平面 中,过点
中,过点 ,作
,作 交
交 于
于 ,取
,取 为坐标原点,分别以
为坐标原点,分别以 ,
,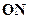 ,
, 所在的直线为
所在的直线为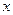 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系
轴,建立空间直角坐标系 (如图所示) …………1分
(如图所示) …………1分
则
 为
为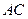 中点,
中点, …………2分
…………2分
设
 .
.


 即
即 ,
, . …………6分
. …………6分
所以存在点 使得
使得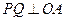 且
且 . …………8分
. …………8分
(2)记平面 的法向量为
的法向量为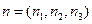 ,则由
,则由 ,
, ,且
,且 ,
,
得 , 故可取
, 故可取 …………10分
…………10分
又平面 的法向量为
的法向量为 . …………11分
. …………11分
 . …………13分
. …………13分
二面角 的平面角是锐角,记为
的平面角是锐角,记为 ,则
,则 …………14分
…………14分
 内作
内作 交
交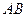 于
于 ,连接
,连接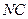 .…………1分
.…………1分
又
 ,
, 
 ,
,  。
。 
取
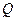 为
为 的中点,则
的中点,则
 …………4分
…………4分在等腰
 中,
中, ,
, 
在
 中,
中, ,
, ……4分
……4分在
 中,
中, ,
,  …5分
…5分 …………8分
…………8分(2)连接
 ,
,由
 ,
,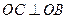 知:
知: .
.又
 ,
,
又由
 ,
, .
.又

 ,
,
又

 是
是 的中点,
的中点,

 ,
, ,
, ,
,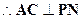
 为二面角
为二面角 的平面角 …………10分
的平面角 …………10分在等腰
 中,
中, ,
,
在
 中,
中, ,
, 在
在 中,
中,  . …………12分
. …………12分 …………14分
…………14分
解法二:在平面
 中,过点
中,过点 ,作
,作 交
交 于
于 ,取
,取 为坐标原点,分别以
为坐标原点,分别以 ,
,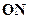 ,
, 所在的直线为
所在的直线为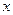 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系
轴,建立空间直角坐标系 (如图所示) …………1分
(如图所示) …………1分则

 为
为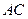 中点,
中点, …………2分
…………2分设

 .
.

 即
即 ,
, . …………6分
. …………6分所以存在点
 使得
使得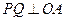 且
且 . …………8分
. …………8分(2)记平面
 的法向量为
的法向量为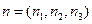 ,则由
,则由 ,
, ,且
,且 ,
,得
 , 故可取
, 故可取 …………10分
…………10分又平面
 的法向量为
的法向量为 . …………11分
. …………11分 . …………13分
. …………13分二面角
 的平面角是锐角,记为
的平面角是锐角,记为 ,则
,则 …………14分
…………14分略

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目

 的法向量
的法向量 ,平面
,平面 的法向量
的法向量 ,若
,若 ,则k的值为
,则k的值为

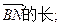
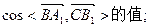
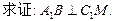
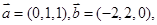 ,则向量
,则向量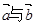 的夹角为
的夹角为



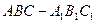 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ,侧棱
,侧棱 ,D,E分别是
,D,E分别是 与
与 的中点,点E在平面ABD上的射影是
的中点,点E在平面ABD上的射影是 的重心G.则
的重心G.则
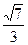


 ,且l的方向向量为(2, m, 1), 平面
,且l的方向向量为(2, m, 1), 平面 , 2), 则m= .
, 2), 则m= .