题目内容
在直三棱柱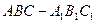 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ,侧棱
,侧棱 ,D,E分别是
,D,E分别是 与
与 的中点,点E在平面ABD上的射影是
的中点,点E在平面ABD上的射影是 的重心G.则
的重心G.则 与平面ABD所成角的余弦值 ( )
与平面ABD所成角的余弦值 ( )
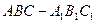 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ,侧棱
,侧棱 ,D,E分别是
,D,E分别是 与
与 的中点,点E在平面ABD上的射影是
的中点,点E在平面ABD上的射影是 的重心G.则
的重心G.则 与平面ABD所成角的余弦值 ( )
与平面ABD所成角的余弦值 ( )A. | B.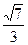 | C. | D. |
B
以C为坐标原点,CA所在直线为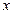 轴,CB所在直线为
轴,CB所在直线为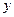 轴,
轴,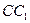 所在直线为
所在直线为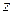 轴,建立直角坐标系,
轴,建立直角坐标系,
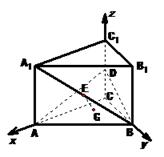
设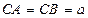 ,
,
则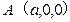 ,
,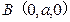 ,
,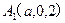 ,
,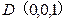
∴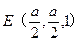 ,
, 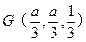 ,
, 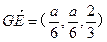 ,
,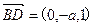 ,
,
∵点E在平面ABD上的射影是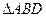 的重心G,
的重心G,
∴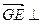 平面ABD, ∴
平面ABD, ∴ ,解得
,解得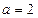 .
.
∴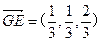 ,
, 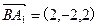 ,
,
∵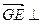 平面ABD,∴
平面ABD,∴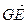 为平面ABD的一个法向量.
为平面ABD的一个法向量.
由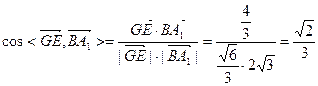
∴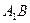 与平面ABD所成的角的余弦值为
与平面ABD所成的角的余弦值为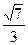 .
.
评析 因规定直线与平面所成角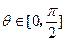 ,两向量所成角
,两向量所成角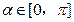 ,所以用此法向量求出的线面角应满足
,所以用此法向量求出的线面角应满足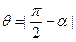 .
.
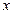 轴,CB所在直线为
轴,CB所在直线为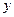 轴,
轴,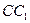 所在直线为
所在直线为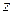 轴,建立直角坐标系,
轴,建立直角坐标系,
设
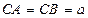 ,
,则
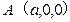 ,
,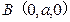 ,
,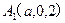 ,
,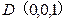
∴
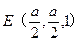 ,
, 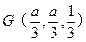 ,
, 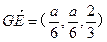 ,
,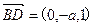 ,
, ∵点E在平面ABD上的射影是
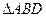 的重心G,
的重心G,∴
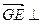 平面ABD, ∴
平面ABD, ∴ ,解得
,解得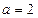 .
.∴
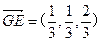 ,
, 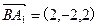 ,
,∵
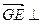 平面ABD,∴
平面ABD,∴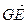 为平面ABD的一个法向量.
为平面ABD的一个法向量.由
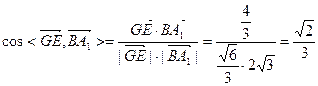
∴
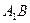 与平面ABD所成的角的余弦值为
与平面ABD所成的角的余弦值为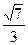 .
.评析 因规定直线与平面所成角
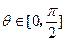 ,两向量所成角
,两向量所成角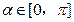 ,所以用此法向量求出的线面角应满足
,所以用此法向量求出的线面角应满足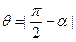 .
.
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 中,
中, ,
, ,点
,点 分别是
分别是 的中点,
的中点, 底面
底面 .
. 平面
平面 ;
; 时,求直线
时,求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值; 为何值时,
为何值时, 在平面
在平面 的重心.
的重心.
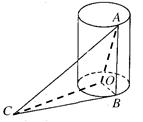
 ,M是棱
,M是棱 的中点,N是棱
的中点,N是棱 的中点.
的中点. 所成角的正弦值;
所成角的正弦值; 的体积.
的体积.
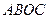 中,
中,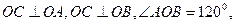 且
且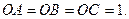
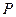 为
为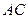 的中点,证明:在
的中点,证明:在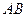 上存在一点
上存在一点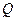 ,使
,使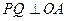 ,并计算
,并计算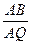 的值;
的值;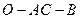 的平面角的余弦值.
的平面角的余弦值. 
 中,
中, 是正三角形,
是正三角形, ,D是
,D是 的中点,二面角
的中点,二面角 为120,
为120, ,
, .取AC的中点O为坐标原点建立空间直角坐标系,如图所示,BD交z轴于点E.
.取AC的中点O为坐标原点建立空间直角坐标系,如图所示,BD交z轴于点E.
 ,
, ; (2)
; (2)  ,
, ;
; ,
, ; (4)
; (4) ,
,